
| A. | ①④⑤ | B. | ③④⑤ | C. | ④⑤⑥ | D. | ②⑤⑥ |
分析 根据一元二次方程的定义对各小题进行逐一判断即可.
解答 解:①x+y=x2是二元二次方程,故本小题错误;
②$\frac{{x}^{3}}{x}$-x=0是分式方程,故本小题错误;
③(x2-1)(x+1)=x(5+x)是一元三次方程,故本小题错误;
④$\sqrt{5}$t2-6t=0是一元二次方程,故本小题正确;
⑤y2=6是一元二次方程,故本小题正确;
⑥$\frac{x}{3}$-1=$\frac{{x}^{2}}{4}$是一元二次方程,故本小题正确.
故选A.
点评 本题考查的是一元二次方程的定义,熟知只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程是解答此题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{y=5x+5}\\{y-6=6x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y+5=5x}\\{y=6x-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+5=5x}\\{y=6x+6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=5x+5}\\{y+6=6x}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
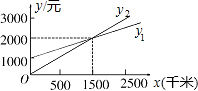 某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司的一家签定月租车合同,设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费是y2元,yl、y2分别与x之间的函数关系图象 (两条射线)如图所示,当每月行驶的路程等于1500时,租两家的费用相同?
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司的一家签定月租车合同,设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费是y2元,yl、y2分别与x之间的函数关系图象 (两条射线)如图所示,当每月行驶的路程等于1500时,租两家的费用相同?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
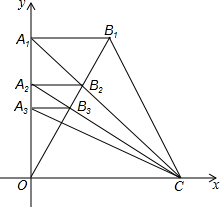 在平面直角坐标系中,直角梯形OA1B1C的位置如图所示,A1的坐标为(0,2),点C的坐标为(2,0),tan∠OCB1=2,连接A1C交OB1于点B2,作A2B2⊥y轴于点A2,得到第二个直角梯形OA2B2C,连接A2C交OB1于点B3,同样办法得到第三个直角梯形OA3B3C,…以此类推,第n个直角梯形顶点Bn的坐标为($\frac{1}{12}$n2-$\frac{7}{12}$n+$\frac{3}{2}$,$\frac{1}{6}$n2-$\frac{7}{6}$n+3).
在平面直角坐标系中,直角梯形OA1B1C的位置如图所示,A1的坐标为(0,2),点C的坐标为(2,0),tan∠OCB1=2,连接A1C交OB1于点B2,作A2B2⊥y轴于点A2,得到第二个直角梯形OA2B2C,连接A2C交OB1于点B3,同样办法得到第三个直角梯形OA3B3C,…以此类推,第n个直角梯形顶点Bn的坐标为($\frac{1}{12}$n2-$\frac{7}{12}$n+$\frac{3}{2}$,$\frac{1}{6}$n2-$\frac{7}{6}$n+3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com