
| ����x | 1 | 2 | 3 | 4 |
| �۸�y1��Ԫ/Ͱ�� | 60 | 59 | 58 | 57 |
���� ��1�����ݱ������ݣ��ɵó�y1��x�ĺ�����ϵʽ�����㣨1��54������2��57�����룬�ɵó�y2��x�ĺ�����ϵʽ��
��2���ֱ�ó�9�·ݡ�10�·ݵ��������ʽ��Ȼ�������䷽�������ֵ���̶��ȽϿɵó��𰸣�
��3���������⣬��x=2���m2����x=3���y2��Ȼ���г����̣����a��ֵ���ɣ�ע�⿼��ʵ���������ȡ�ᣮ
��� �⣺��1��9�·ݣ����ݱ���ɵã�y1=-x+61��
10�·ݣ��ߵ�x=1ʱ��y=54����x=2ʱ��y=57��
��$\left\{\begin{array}{l}{b+c-\frac{1}{4}=54}\\{2b+c-1=57}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=\frac{15}{4}}\\{c=\frac{101}{2}}\end{array}\right.$��
��y2=-$-\frac{1}{4}$x2+$\frac{15}{4}$x+$\frac{101}{2}$��
��2�����x�ܵ�����ΪwԪ��
9�·ݣ�w=y1-m1=��-x+61��-�� $\frac{1}{3}$x2-3x+50��=-$\frac{1}{3}$x2+2x+11=-$\frac{1}{3}$��x-3��2+14��
��-$\frac{1}{3}$��0��
������£�
�֡߶Գ����ǣ�ֱ��x=3��
�൱x=3ʱ��w���=14��
10�·ݣ�w=y2-m2=-$\frac{1}{4}$x2+$\frac{15}{4}$x+$\frac{101}{2}$-�� $\frac{7}{2}$x+$\frac{81}{2}$��=-$\frac{1}{4}$x2+$\frac{1}{4}$x=10=-$\frac{1}{4}$��x-$\frac{1}{2}$��2+$\frac{161}{16}$
��-$\frac{1}{4}$��0��
������£�
�֡߶Գ����ǣ�ֱ��x=$\frac{1}{2}$��
�൱1��x��4ʱ��w��x���������С��
�൱x=1ʱ��w���=10��
��14��10��
��9�·ݵĵ�3�ܣ���������������Ϊ14Ԫ/Ͱ��
��3����m2=$\frac{7}{2}$x+$\frac{81}{2}$�У���x=2���ã�m2=$\frac{95}{2}$��
��y2=-$\frac{1}{4}$x2+$\frac{15}{4}$x+$\frac{101}{2}$�У���x=3���ã�y2=$\frac{119}{2}$��
��$\frac{119}{2}$��1200•3a%+$\frac{119}{2}$��1-a%��•1200•��1-3a%��-$\frac{95}{2}$��1200=12000��
��a%=m����357m+119��1-m����1-3m��=115��
�����ã�357m2-119m+4=0��
��=8449��922��
m1��$\frac{119+92}{714}$��0.295��
��a1��30���������⣬��ȥ����
m2��$\frac{119-92}{714}$��0.037��
��a2��4��
��a������ֵΪ4��
���� ���⿼���˶��κ�����Ӧ�ã���Ŀ������Ϣ���Ƚϴ�ע����ϸ���⣬�õ�������Ҫ����Ϣ����ʵ������ת��Ϊ��ѧģ�ͽ�����⣬�ѶȽϴ�


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$\frac{1}{3}{x}^{2}$ | B�� | y=$\sqrt{{x}^{2}-1}$ | C�� | y=$\frac{1}{{x}^{2}}$ | D�� | y=ax2+bx+c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����εĽ�ƽ���ߡ����ߡ��߶��������ε��ڲ� | |
| B�� | �����εĽ�ƽ���ߡ��߶��������ε��ڲ� | |
| C�� | �����εĸߡ����߶��������ε��ڲ� | |
| D�� | �����εĽ�ƽ���ߡ����߶��������ε��ڲ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+x+1=0 | B�� | 2x2-3x+5=0 | C�� | x2-7x=8 | D�� | x2+6x+7=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
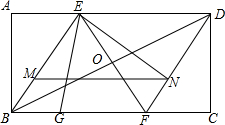 ��֪��ͼ������ABCD�ĶԽ���BD���д��߷ֱ�AD��BC���ڵ�E��F������EB��DF��AB=$\sqrt{3}$��AD=3��
��֪��ͼ������ABCD�ĶԽ���BD���д��߷ֱ�AD��BC���ڵ�E��F������EB��DF��AB=$\sqrt{3}$��AD=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��������IJ�ֵ����λ��g�� | -8 | -3 | 0 | 2 | 4 |
| ��� | 4 | 3 | 6 | 2 | 1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com