
 如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.则⊙O的半径是5;若点E为圆上一点,∠ECD=15°,将$\widehat{CE}$沿弦CE翻折,交CD于点F图中阴影部分的面积是$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$. 分析 根据AB⊥CD,垂足为G,OG:OC=3:5,AB=8,可以求得⊙O的半径;要求阴影部分的面积只要做出合适的辅助线,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.
解答 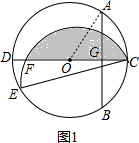 解:连接AO,如右图1所示,
解:连接AO,如右图1所示,
∵CD为⊙O的直径,AB⊥CD,AB=8,
∴AG=$\frac{1}{2}$=4,
∵OG:OC=3:5,AB⊥CD,垂足为G,
∴设⊙O的半径为5k,则OG=3k,
∴(3k)2+42=(5k)2,
解得,k=1或k=-1(舍去),
∴5k=5,
即⊙O的半径是5;
如图2所示,将阴影部分沿CE翻折,点F的对应点为M,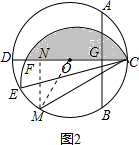
∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,
连接OM,则∠MOD=60°,
∴∠MOC=120°,
过点M作MN⊥CD于点N,
∴MN=MO•sin60°=5×$\frac{\sqrt{3}}{2}$,
∴S阴影=S扇形OMC-S△OMC=$\frac{120×π×{5}^{2}}{360}$-$\frac{25\sqrt{3}}{4}$=$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$,
即图中阴影部分的面积是:$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
故答案为:5,$\frac{25π}{3}$-$\frac{25\sqrt{3}}{4}$.
点评 本题考查垂径定理、扇形的面积、翻折变换,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=-$\frac{1}{2}$.下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=-$\frac{1}{2}$.下列结论:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A同学 | 5 | 8 | 8 | 9 | 8 | 10 | 9 | 8 | 8 | 5 |
| B同学 | 10 | 7 | 7 | 9 | 10 | 5 | 8 | 6 | 10 | 8 |
| 同学 | 平均分 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
| A | 7.8 | b | 8 | 2.36 | 80% | f |
| B | a | 7 | c | d | e | 40% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com