

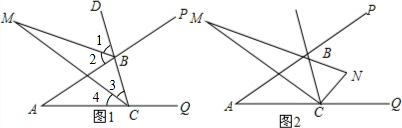
 解:(1)∵在△ABC中,∠ABD=∠A+∠ACB,
解:(1)∵在△ABC中,∠ABD=∠A+∠ACB,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,⊙O中延长半径CO交弦AB于点P,∠OAB=30°,设∠OCB=α,∠COA=β.
如图,⊙O中延长半径CO交弦AB于点P,∠OAB=30°,设∠OCB=α,∠COA=β.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在物理知识中,压强P与受力面积S成反比例,点(2,7.5)在该函数图象上.
如图,在物理知识中,压强P与受力面积S成反比例,点(2,7.5)在该函数图象上.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,两个等圆⊙O1和⊙O2互过圆心,且交于A、B两点,点P是⊙O2上任意一点(不与A、B重合),则∠APB的度数为( )
如图,两个等圆⊙O1和⊙O2互过圆心,且交于A、B两点,点P是⊙O2上任意一点(不与A、B重合),则∠APB的度数为( )| A、60°或120° |
| B、30°或150° |
| C、60° |
| D、30° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 《中华人民共和国道路交通管理条例》规定:“小汽车在城市街道上的行驶速度不得超过70千 米/时”.一辆小汽车在一条城市街道上由西向东行驶(如图所示),在距离路边OC=30米处有“车速检测仪O”,测得该车从北偏西60°的A点行驶到北偏西30°的B点,所用时间为2秒.这辆“小汽车”超速了吗?请说明理由.(参考数据:
《中华人民共和国道路交通管理条例》规定:“小汽车在城市街道上的行驶速度不得超过70千 米/时”.一辆小汽车在一条城市街道上由西向东行驶(如图所示),在距离路边OC=30米处有“车速检测仪O”,测得该车从北偏西60°的A点行驶到北偏西30°的B点,所用时间为2秒.这辆“小汽车”超速了吗?请说明理由.(参考数据:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| ||
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com