
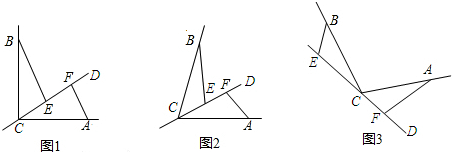
分析 (1)①求出∠BEC=∠AFC=90°,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;②求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;
(2)求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可.
解答 解:(1)①如图1中,
E点在F点的左侧,∵BE⊥CD,AF⊥CD,∠ACB=90°,
∴∠BEC=∠AFC=90°,
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠EBC=∠ACF}\\{∠BEC=∠AFC}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF-CE=BE-AF,
当E在F的右侧时,同理可证EF=AF-BE,
∴EF=|BE-AF|;
故答案为=,=.
②∠α+∠ACB=180°时,①中两个结论仍然成立;
证明:如图2中,
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠EBC=∠ACF}\\{∠BEC=∠AFC}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF-CE=BE-AF,
当E在F的右侧时,同理可证EF=AF-BE,
∴EF=|BE-AF|;
(2)EF=BE+AF.
理由是:如图3中,
∵∠BEC=∠CFA=∠a,∠a=∠BCA,
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,
∴∠EBC+∠BCE=∠BCE+∠ACF,
∴∠EBC=∠ACF,
在△BEC和△CFA中,
$\left\{\begin{array}{l}{∠EBC=∠FCA}\\{∠BEC=∠CFA}\\{BC=CA}\end{array}\right.$,
∴△BEC≌△CFA(AAS),
∴AF=CE,BE=CF,
∵EF=CE+CF,
∴EF=BE+AF.
点评 本题综合考查三角形综合题、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,注意这类题目图形发生变化,结论基本不变,证明方法完全类似,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
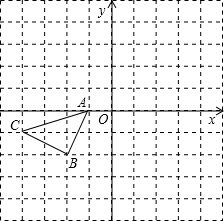 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数为10,方差是2 | B. | 平均数是11,方差为4 | ||
| C. | 平均数为11,方差为2 | D. | 平均数为12,方差为4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35 | B. | 38 | C. | 48 | D. | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 父母恩情似海深,人生莫忘父母恩,乐陵市教育局为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全市范围内随机抽取了若干名中小学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
父母恩情似海深,人生莫忘父母恩,乐陵市教育局为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全市范围内随机抽取了若干名中小学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com