
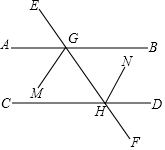
 如图,AB∥CD,MG平分∠AGF,NH平分∠EHD,那么GM∥HN,请说明理由.
如图,AB∥CD,MG平分∠AGF,NH平分∠EHD,那么GM∥HN,请说明理由.  口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
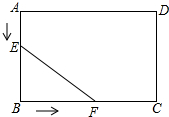 如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.
如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
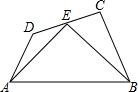 如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$.
如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com