
【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
(1)![]() ________;
________;![]() ________;并求直线
________;并求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

【答案】(1)4,2,![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)先根据非负数的性质可求得a,b的值,利用待定系数法可求得直线AB的解析式;
(2)先求得点M的坐标,过M点作MN⊥OA于点N,MP⊥OB于点P,由题设可证△MNA≌△MPC,△OMN≌△OMP,利用全等的性质可分别求得CP的长,从而求得点C的坐标;
(3)先假设存在点D,设D(a,a),根据S△ABD=6,列出关于a方程,若有解则存在,无解则不存在,要注意分两种情况考虑.
(1)∵![]()
∴a-4=0,b-2=0
即a=4,b=2
∴A(4,0),B(0,2)
设直线AB的解析式为y=kx+b,将![]() ,
,![]() 代入
代入![]() 得
得
![]() ,
,
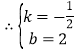
![]() 直线
直线![]() 解析式为
解析式为![]()
(2)联立方程组得,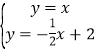 ,
,
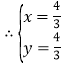 ,
,
即![]()
如图1,过M点作MN⊥OA于点N,MP⊥OB于点P,
则四边形OPMN是矩形,
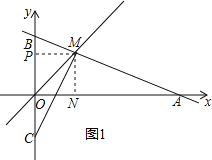
由点M的坐标可知MN=MP,
∴矩形OPMN是正方形,
∴∠PMN=90°,∠MPC=∠MNA=90°,
又∠OMA=90°,
∴∠PMC=∠NMA,
∴△MNA≌△MPC,△OMN≌△OMP,
则CP=AN,OP=ON=![]() ,
,
而CP=AN=OA-ON=![]() ,
,
故OC=![]() ,
,
所以C(0,![]() );
);
(3)存在点D.
∵D在y=x上
∴设D(a,a)
①如图2,若D在AB的下方,
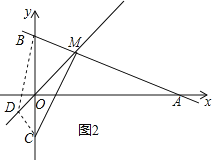
∵S△AOB=4,S△ABD=6
∴D在MO的延长线上
∴S△AOD+S△BOD+S△AOB=S△ABD,
∴![]() (AO+BO)|a|+4=6,
(AO+BO)|a|+4=6,
∴-![]() ×6a=2,
×6a=2,
解得:a=-![]() ,
,
∴D(![]() ,
,![]() )
)
②若D在AB的上方同理求得D′(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,以正方形![]() 的顶点
的顶点![]() 为坐标原点,直线
为坐标原点,直线![]() 为
为![]() 轴建立直角坐标系,对角线
轴建立直角坐标系,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上一点,点
上一点,点![]() 坐标为
坐标为![]() ,则点
,则点![]() 绕点
绕点![]() 顺时针旋转90°得到的对应点
顺时针旋转90°得到的对应点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在直线1上,AB = 20cm,∠BAC= 120°.

(1)点P从A出发,沿射线AB以每秒2cm的速度向右运动,同时点Q从B出发,沿射线BA以每秒lcm的速度向左运动,求点P出发多少秒时与点Q重合?
(2)在(1)的条件下,求点P出发多少秒时与点Q相距5cm?
(3)点M为射线AC上一点,AM = 4cm,现将射线AC绕点A以每秒30°的速度顺时针旋转一周后停止,同时点N从点B出发沿直线AB向左运动,在这一运动过程中,是否存在某一时刻,使得点N为BM的中点?若存在,求出点N运动的速度:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面的情景,回答问题:
小王逛超市看到如下两个超市的促销信息

备注:假设两家超市相同的标价都一样.
(1)当一次性购买标价总额是400元时,甲、乙超市实际付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款189元和474元,若他只去一次该超市购买同样多的商品,可以节省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
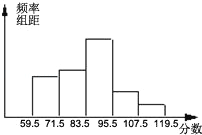
【题目】我市某区对参加市模拟考试的8000名学生的数学成绩进行抽样调查,抽取了部分学生的数学成绩(分数为整数)进行统计,绘制成频率分布直方图.如下图,已知从左到右五个小组的频数是之比依次是6:7:11:4:2,第五小组的频数是40.
(1)本次调查共抽取了多少名学生?
(2)若72分以上(含72分)为及格,96分以上(含96分)为优秀,那么抽取的学生中,及格的人数、优秀的人数各占所抽取的学生数的百分之多少?
(3)根据(2)的结论,该区所有参加市模拟考试的学生,及格人数、优秀人数各约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号 | 方程 | 方程的解 |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
… | … | … |
(1)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
(2)请写出这列方程中第n个方程:_____ 方程的解:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )

A.5B.6C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com