练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF； ②AB=DE，∠B=∠E，BC=EF；③∠B=∠E，BC=EF，∠C=∠F； ④AB=DE，AC=DF，∠B=∠E．能使△ABC≌△DEF有_____组．

    【答案】3.

    【解析】

    根据全等三角形的判定方法逐一判断即可.

    解：①已知AB=DE，BC=EF，AC=DF；根据SSS可判定△ABC≌△DEF；

    ②已知AB=DE，∠B=∠E，BC=EF；根据SAS可判定△ABC≌△DEF；

    ③已知∠B=∠E，BC=EF，∠C=∠F；根据ASA可判定△ABC≌△DEF；

    ④已知AB=DE，AC=DF，∠B=∠E；不能由边边角判定两个三角形全等.

    故能判定△ABC≌△DEF的有3组，故答案为3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知蜗牛从点出发，在一条数轴上来回爬行，规定：向正半轴运动记作“+”，向负半轴运动记作“-”，从开始到结束爬行的各段路程（单位：）依次为：+7，-5，-10，-8，+9，-6，+12，+4．

    （1）若点在数轴上表示的数为-3，则蜗牛停在数轴上何处，请通过计算加以说明；

    （2）蜗牛在（1）题在数轴上停的位置作以下运动：第1次向左移动1个单位长度至点，第2次从点向右移动2个单位长度至点，第3次从点向左移动3个单位长度至点，第4次从点向右移动4个单位长度至点，…，依此类推．这样第2019次移动到的点在数轴上表示的数为（请直接写出答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，CA＝CB＝5，AB＝6，AB⊥y轴，垂足为A．反比例函数y＝（x＞0）的图象经过点C，交AB于点D．

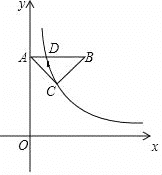
    （1）若OA＝8，求k的值；

    （2）若CB＝BD，求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠A=160°．第一步：在△ABC上方确定一点A1，使∠A1BA=∠ABC，∠A1CA=∠ACB，如图1，则∠A1的度数为__；第二步：在△A1BC上方确定一点A2，使∠A2BA1=∠A1BA，∠A2CA1=∠A1CA，如图2．照此下去，至多能进行___步．

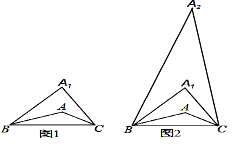
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，∠OCD＝60°，连接OD．

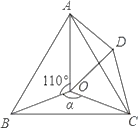
    （1）求证：△OCD是等边三角形；

    （2）当α＝150°时，试判断△AOD的形状，并说明理由；

    （3）探究：当α为多少度时，△AOD是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司根据市场计划调整投资策略，对A、B两种产品进行市场调查，收集数据如下表：

    项目

    产品

    年固定成本

    （单位：万元）

    每件成本

    （单位：万元）

    每件产品销售价

    （万元）

    每年最多可生产的件数

    A

    20

    m

    10

    200

    B

    40

    8

    18

    120

    其中，m是待定系数，其值是由生产A的材料的市场价格决定的，变化范围是6≤m＜8，销售B产品时需缴纳x2万元的关税．其中，x为生产产品的件数．假定所有产品都能在当年售出，设生产A，B两种产品的年利润分别为y1、y2（万元）．

    （1）写出y1、y2与x之间的函数关系式，注明其自变量x的取值范围．

    （2）请你通过计算比较，该公司生产哪一种产品可使最大年利润更大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点，以AB为直径的⊙P经过该抛物线的顶点C，直线l∥ x轴，交该抛物线于M、N两点，交⊙ P与E、F两点，若EF=2，则MN的长是_____．

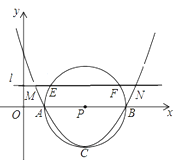
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的情境对话，然后解答问题

    （1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？

    （2）在RtABC 中， ∠ACB＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若RtABC是奇异三角形，求a：b：c；

    （3）如图，AB是⊙O的直径，C是上一点（不与点A、B重合），D是半圆的中点，CD在直径AB的两侧，若在⊙O内存在点E使得AE＝AD，CB＝CE．

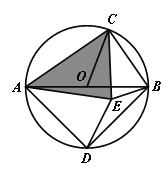
    求证：ACE是奇异三角形；

    当ACE是直角三角形时，求∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】元旦放假时，小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥．早上从家里出发，向东走了5千米到超市买东西，然后又向东走了2.5千米到爷爷家，下午从爷爷家出发向西走了10千米到姥爷家，晚上返回家里．

    （1）若以小明家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来；

    （2）超市和姥爷家相距多少千米？

    （3）若小轿车每千米耗油0.08升，求小明一家从出发到返回家，小轿车的耗油量．

    查看答案和解析>>

    同步练习册答案