
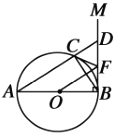
【题目】如图,![]() 为
为![]() 的直径,直线
的直径,直线![]() 于点
于点![]() .点
.点![]() 在
在![]() 上,分别连接
上,分别连接![]() ,
,![]() ,且
,且![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() 为
为![]() 的切线交
的切线交![]() 于点
于点![]() .
.

(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据切线的性质得![]() ,由切线长定理可证
,由切线长定理可证![]() ,从而
,从而![]() ,然后根据等角的余角相等得到
,然后根据等角的余角相等得到![]() ,从而根据等腰三角形的判定定理得到结论;
,从而根据等腰三角形的判定定理得到结论;
(2)根据勾股定理计算出AC=8,再证明△ABC∽△ABD,利用相似比得到AD=![]() ,然后证明OF为△ABD的中位线,从而根据三角形中位线性质求出OF的长.
,然后证明OF为△ABD的中位线,从而根据三角形中位线性质求出OF的长.
(1)证明:∵![]() 是
是![]() 的直径,
的直径,
∴![]() (直径所对的圆周角是
(直径所对的圆周角是![]() ),
),
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,![]() 于点
于点![]() ,
,
∴![]() 是
是![]() 的切线(经过半径外端且与半径垂直的直线是圆的切线),
的切线(经过半径外端且与半径垂直的直线是圆的切线),
∵![]() 是
是![]() 的切线,
的切线,
∴![]() (切线长定理),
(切线长定理),
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() .
.
(2)由(1)可知,![]() 是直角三角形,在
是直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理求得![]() ,
,
在![]() 和
和![]() 中
中
![]() ,
,
∴![]() (两个角对应相等的两个三角形相似),
(两个角对应相等的两个三角形相似),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() (三角形的中位线平行于第三边并且等于第三边的一半).
(三角形的中位线平行于第三边并且等于第三边的一半).


科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD.
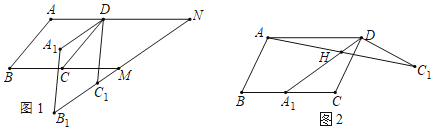
(1)如图1,将ABCD绕点D逆时针旋转一定角度得到A1B1C1D,延长B1C1,分别与BC、AD的延长线交于点M、N.
①求证:∠BMB1=∠ADA1;
②求证:B1N=AN+C1M;
(2)如图2,将线段AD绕点D逆时针旋转,使点A的对应点A1落在BC上,将线段CD绕点D逆时针旋转到C1D的位置,AC1与A1D交于点H.若H为AC1的中点,∠ADC1+∠A1DC=180°,A1B=nA1C,试用含n的式子表示![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
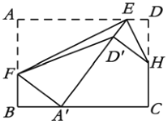
【题目】如图,矩形纸片![]() 中,
中,![]() ,
,![]() ,将纸片沿
,将纸片沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,折痕分别交边
处,折痕分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() .再将纸片沿
.再将纸片沿![]() 折叠,使点
折叠,使点![]() 落在线段
落在线段![]() 上的
上的![]() 处,折痕交边
处,折痕交边![]() 于点
于点![]() .连接
.连接![]() ,则
,则![]() 的长是______
的长是______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
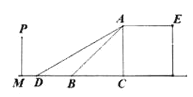
【题目】某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求舞台的高AC(结果保留根号)
(2)楼梯口B左侧正前方距离舞台底部C点3m处的文化墙PM是否要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校自主开发了A书法、B阅读,C绘画,D器乐四门选修课程供学生选择,每门课程被选到的机会均等.
(1)若学生小玲计划选修两门课程,请写出她所有可能的选法;
(2)若学生小强和小明各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
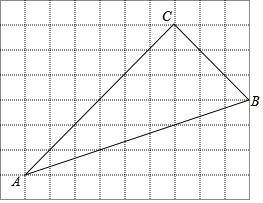
【题目】如图,在边长为1个单位长度的小正方形组成的8×10网格中,点A,B,C均为网格线的交点.
(1)用无刻度的直尺作BC边上的中线AD(不写作法,保留作图痕迹);
(2)①在给定的网格中,以A为位似中心将△ABC缩小为原来的![]() ,得到△AB′C′,请画出△AB′C′.
,得到△AB′C′,请画出△AB′C′.
②填空:tan∠AD′C'= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元.市场调査发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com