
某水果店销售某中水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2﹣8mx+n,其变化趋势如图2.
(1)求y2的解析式;
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?
(1) y2=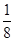 x2﹣x+
x2﹣x+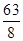 (1≤x≤12);(2) 第3月销售这种水果,每千克所获得利润最大,最大利润是
(1≤x≤12);(2) 第3月销售这种水果,每千克所获得利润最大,最大利润是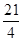 元/千克.
元/千克.
解析试题分析:(1)把函数图象经过的点(3,6),(7,7)代入函数解析式,解方程组求出m、n的值,即可得解;
(2)根据图1求出每千克的售价y1与x的函数关系式,然后根据利润=售价﹣成本得到利润与x的函数关系式,然后整理成顶点式形式,再根据二次函数的最值问题解答即可.
试题解析:(1)由图可知,y2=mx2﹣8mx+n经过点(3,6),(7,7),
∴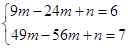 ,
,
解得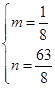 .
.
∴y2=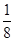 x2﹣x+
x2﹣x+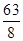 (1≤x≤12);
(1≤x≤12);
(2)设y1=kx+b(k≠0),
由图可知,函数图象经过点(4,11),(8,10),
则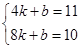 ,
,
解得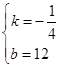 ,
,
所以,y1=﹣ x+12,
x+12,
所以,每千克所获得利润=(﹣ x+12)﹣(
x+12)﹣(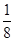 x2﹣x+
x2﹣x+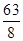
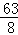 )
)
=﹣ x+12﹣
x+12﹣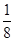 x2+x﹣
x2+x﹣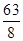
=﹣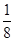 x2+
x2+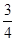 x+
x+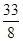
=﹣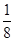 (x2﹣6x+9)+
(x2﹣6x+9)+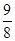 +
+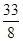
=﹣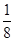 (x﹣3)2+
(x﹣3)2+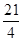 ,
,
∵﹣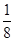 <0,
<0,
∴当x=3时,所获得利润最大,为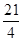 元.
元.
答:第3月销售这种水果,每千克所获得利润最大,最大利润是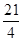 元/千克.
元/千克.
【考点】二次函数的应用.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
我市高新技术开发区的某公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-投资成本)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该公司希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利不低于1842元,请你确定此时销售单价的范围.在此情况下,要使产品销售量最大,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,抛物线y=x2﹣(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.
(1)若m=2,n=1,求A、B两点的坐标;
(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,﹣1),求∠ACB的大小;
(3)若m=2,△ABC是等腰三角形,求n的值.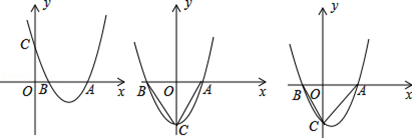
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系 中,二次函数
中,二次函数 (
(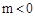 )的图象与
)的图象与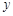 轴正半轴交于A点.
轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数 (a≠0)的图象经过点A,点B.
(a≠0)的图象经过点A,点B.
(1)求二次函数的表达式;
(2)若反比例函数 (x>0)的图象与二次函数
(x>0)的图象与二次函数 (a≠0)的图象在第一象限内交于点
(a≠0)的图象在第一象限内交于点 ,
, 落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
(3)若反比例函数 (x>0,k>0)的图象与二次函数
(x>0,k>0)的图象与二次函数 (a≠0)的图象在第一象限内交于点
(a≠0)的图象在第一象限内交于点 ,且
,且 ,试求实数k的取值范围.
,试求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线 与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
(1)求抛物线的解析式;
(2)设点P的横坐标为m.
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为1:2.若存在,直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,已知二次函数 的图象与
的图象与 轴相交于点
轴相交于点 ,顶点为
,顶点为 ,点
,点 在这个二次函数图象的对称轴上.若四边形
在这个二次函数图象的对称轴上.若四边形 是一个边长为2且有一个内角为
是一个边长为2且有一个内角为 的菱形.求此二次函数的表达式.
的菱形.求此二次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com