
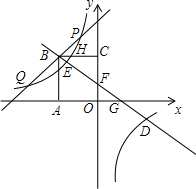
 如图,正方形ABCO的顶点A,C分别在x轴,y轴上,O为坐标原点,点B在第二象限,边长为m,双曲线线y=$\frac{k}{x}$(x≠0)经过BC的中点H.
如图,正方形ABCO的顶点A,C分别在x轴,y轴上,O为坐标原点,点B在第二象限,边长为m,双曲线线y=$\frac{k}{x}$(x≠0)经过BC的中点H.分析 (1)只需求出点H的坐标,然后代入y=$\frac{k}{x}$就可解决问题;
(2)作EM⊥x轴于M,DN⊥y轴于N,如图1.要证GE=DF,只需证△MEG≌△NFD,易得∠EGM=∠FDN,∠EMG=∠FND,只需证MG=DN.由m=3可得k=-$\frac{9}{2}$,从而得到反比例函数的表达式为y=-$\frac{9}{2x}$.可设E的坐标是(a,-$\frac{9}{2a}$),D的坐标是(b,-$\frac{9}{2b}$),然后运用待定系数法求出直线BD的表达式,求出点G的横坐标,即可得到MG=DN,问题得以解决;
(3)通过度量可得PQ约为PM+QN的1.414倍,由此可以猜想PQ=$\sqrt{2}$(PM+QN).过点P作PS∥x轴,交直线AC于S,过点Q作QR∥x轴,交直线AC于R,如图2.易证PS+QR=$\sqrt{2}$PM+$\sqrt{2}$QN=$\sqrt{2}$(PM+QN),只需证到PQ=PS+QR即可.可用待定系数法依次求出直线AC为y=x+3、直线PQ的表达式为y=k′x+3k′+3.,设点P的坐标为(x1,y1),点Q的坐标为(x2,y2),易得PS+QR=(k′-1)(x1+x2)+6k′.由P(x1,y1),Q(x2,y2)是直线y=k′x+3k′+3与双曲线y=-$\frac{9}{2x}$的交点,可得x1、x2是方程k′x+3k′+3=-$\frac{9}{2x}$即2k′x2+6(k′+1)x+9=0的解,根据根与系数的关系可得x1+x2=-$\frac{3(k′+1)}{k′}$,x1•x2=$\frac{9}{2k′}$,从而得到PS+QR=$\frac{3(k{′}^{2}+1)}{k′}$,PQ2=(x1-x2)2+(y1-y2)2=(k′2+1)(x1-x2)2=(k′2+1)[(x1+x2)2-4x1x2]=$\frac{9(k{′}^{2}+1)2}{k{′}^{2}}$,即可得到PQ=$\frac{3(k{′}^{2}+1)}{k′}$,从而得到PQ=PS+QR=$\sqrt{2}$(PM+QN).
解答 解:(1)由题意可得点B的坐标为(-m,m),BC的中点H坐标为(-$\frac{m}{2}$,m).
∵双曲线y=$\frac{k}{x}$(x≠0)经过BC的中点H,
∴k=-$\frac{m}{2}$•m=-$\frac{1}{2}$m2;
(2)作EM⊥x轴于M,DN⊥y轴于N,如图1. ∵k=-$\frac{1}{2}$m2,m=3,
∵k=-$\frac{1}{2}$m2,m=3,
∴k=-$\frac{9}{2}$,
∴反比例函数的表达式为y=-$\frac{9}{2x}$.
设E的坐标是(a,-$\frac{9}{2a}$),D的坐标是(b,-$\frac{9}{2b}$),
则OM=-a,DN=b.
设直线BD的解析式是y=px+q,
则$\left\{\begin{array}{l}{pa+q=-\frac{9}{2a}}\\{pb+q=-\frac{9}{2b}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{p=\frac{9}{2ab}}\\{q=-\frac{9(a+b)}{2ab}}\end{array}\right.$
则直线BD的表达式为y=$\frac{9}{2ab}$x-$\frac{9(a+b)}{2ab}$,
令y=0,解得:x=a+b,
则xG=a+b,
∴MG=a+b-a=b,
∴MG=DN.
∵DN⊥y轴,MG⊥y轴,
∴DN∥MG,
∴∠EGM=∠FDN.
在△MEG和△NFD中,
$\left\{\begin{array}{l}{∠MGE=∠NDF}\\{∠EMG=∠FND}\\{MG=DN}\end{array}\right.$,
∴△MEG≌△NFD(AAS),
∴GE=DF;
(3)PQ=$\sqrt{2}$(PM+QN).
证明:过点P作PS∥x轴,交直线AC于S,过点Q作QR∥x轴,交直线AC于R,如图2.
∵四边形ABCO是正方形,
∴∠CAO=45°.
∵PS∥x轴,QR∥x轴,
∴∠PSA=∠QRA=∠CAO=45°.
∵PM⊥AC,QN⊥AC,
∴PS=$\sqrt{2}$PM,QR=$\sqrt{2}$QN,
∴PS+QR=$\sqrt{2}$PM+$\sqrt{2}$QN=$\sqrt{2}$(PM+QN).
∵m=3,∴A(-3,0)、B(-3,3)、C(0,3).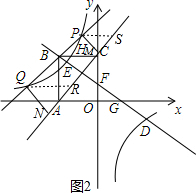
设直线AC的表达式为y=mx+n,
则有$\left\{\begin{array}{l}{-3m+n=0}\\{n=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$,
∴直线AC的表达式为y=x+3.
设直线PQ的表达式为y=k′x+b′,
∵点B在直线PQ上,
∴-3k′+b′=3,
∴b′=3k′+3,
∴直线PQ的表达式为y=k′x+3k′+3.
设点P的坐标为(x1,y1),点Q的坐标为(x2,y2),
则有yS=yP=y1=k′x1+3k′+3,yR=yQ=y2=k′x2+3k′+3,
∴xS+3=y1,xR+3=y2,
∴xS=y1-3,xR=y2-3,
∴PS=y1-3-x1=k′x1+3k′+3-3-x1=(k′-1)x1+3k′,
QR=y2-3-x2=k′x2+3k′+3-3-x2=(k′-1)x2+3k′,
∴PS+QR=(k′-1)(x1+x2)+6k′.
∵P(x1,y1),Q(x2,y2)是直线y=k′x+3k′+3与双曲线y=-$\frac{9}{2x}$的交点,
∴x1、x2是方程k′x+3k′+3=-$\frac{9}{2x}$即2k′x2+6(k′+1)x+9=0的解,
∴x1+x2=-$\frac{6(k′+1)}{2k′}$=-$\frac{3(k′+1)}{k′}$,x1•x2=$\frac{9}{2k′}$
∴PS+QR=(k′-1)•[-$\frac{3(k′+1)}{k′}$]+6k′=6k′-$\frac{3(k{′}^{2}-1)}{k′}$=$\frac{3(k{′}^{2}+1)}{k′}$,
PQ2=(x1-x2)2+(y1-y2)2
=(x1-x2)2+[(k′x1+3k′+3)-(k′x2+3k′+3)]2
=(k′2+1)(x1-x2)2=(k′2+1)[(x1+x2)2-4x1x2]
=(k′2+1)[(-$\frac{3(k′+1)}{k′}$)2-4•$\frac{9}{2k′}$]=$\frac{9(k{′}^{2}+1)2}{k{′}^{2}}$,
∴PQ=$\frac{3(k{′}^{2}+1)}{k′}$,
∴PQ=PS+QR=$\sqrt{2}$(PM+QN).
点评 本题主要考查了运用待定系数法求一次函数及反比例函数的解析式、一次函数及反比例函数图象的交点问题、全等三角形的判定与性质、三角函数、正方形的性质、完全平方公式等知识,对运算能力的要求非常高,解决第(3)小题的关键是先通过度量提出合理的猜想,再用代数方法加以证明.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请你根据图象解答下面的问题:
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请你根据图象解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
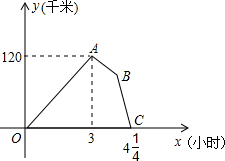 某物流公司的快递车和货车同时从甲地出发,以各自的速度沿平直公路匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度沿平直公路匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com