一组数据2.-2.4.1.0的方差是4．题目和参考答案——青夏教育精英家教网—

14．一组数据2、-2、4、1、0的方差是4．

分析先求出这组数据的平均数，再代入方差公式S²=$\frac{1}{n}$[（x₁-$\overline{x}$）²+（x₂-$\overline{x}$）²+…+（x_n-$\overline{x}$）²]，进行计算即可．

解答解：这组数据的平均数是：（2-2+4+1+0）÷5=1，
则方差=$\frac{1}{5}$[（2-1）²+（-2-1）²+（4-1）²+（1-1）²+（0-1）²]=4．
故答案为：4．

点评本题考查了方差：一般地设n个数据，x₁，x₂，…x_n的平均数为$\overline{x}$，则方差S²=$\frac{1}{n}$[（x₁-$\overline{x}$）²+（x₂-$\overline{x}$）²+…+（x_n-$\overline{x}$）²]．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

4．

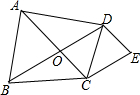如图，O是四边形ABCD对角线的交点，DE∥AC，CE∥BD，若要得到四边形OCED是菱形，已知条件中的四边形要改为（　　）

A．

平行四边形

B．

直角梯形

C．

菱形

D．

矩形

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

5．已知关于x的方程ax+b=c的解是x=1，则|c-a-b-2|=2．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．若m²-2m+10=6n-n²，求[$\frac{m^2-n^2}{m^2+2mn+n^2}$+$\frac{2}{mn}$÷（$\frac{1}{m}$+$\frac{1}{n}$）²]$÷\frac{1}{m+n}$的值．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．下面说法正确的是（　　）

	A．	近似数26.0与26的精确度相同
	B．	近似数3万和近似数30000的精确度相同
	C．	近似数3×10⁴和近似数30000的精确度相同
	D．	近似数3万和3×10⁴的精确度相同

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．阅读以下材料：
对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M$\left\{{-1，2，3}\right\}=\frac{-1+2+3}{3}=\frac{4}{3}$；min{-1，2，3}=-1；min$\left\{{-1，2，a}\right\}=\left\{\begin{array}{l}a\;\;\;\;\;\;\;\;（a≤-1）\\-1\;\;\;\;\;\;\;（a＞-1）.\end{array}$
解决下列问题：
（1）填空：min{sin30°，cos45°，tan30°}=sin30°；
（2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x；
②根据①，你发现了结论：
“如果M{a，b，c}=min{a，b，c}，那么a=b=c（填a，b，c的大小关系）”．
③运用②的结论，填空：
若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=-4．
（3）填空：min{x+1，（x-1）²，2-x}的最大值为1．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

有一只喜鹊在一棵5m高的小树上觅食，它的巢筑在距该树24m的一棵大树上，大树高16m，且巢离树顶部1m，当它听到巢中幼鸟的叫声时，立即赶过去，若它飞行速度为5m/s，则它至少需要多少时间才能赶回巢中？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．当1≤x≤2时，求函数y=-x²-x+1的最大值和最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．计算与化简
（1）a²b³•（ab²）^-2
（2）$\frac{a-b}{a}÷（a-\frac{{2ab-{b^2}}}{a}）$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学