
ЁОЬтФПЁПЮЊЕїВщБОаЃбЇЩњЖдЁАЙиЕЦвЛаЁЪБЁБгаЙиЧщПіЕФСЫНтГЬЖШЃЎбЇаЃеўНЬДІЫцЛњГщШЁВПЗжЭЌбЇНјааСЫЕїВщЃЌНЋЕїВщНсЙћЗжЮЊЃКЁАAЁЊВЛЬЋСЫНтЁЂBЁЊЛљБОСЫНтЁЂCЁЊСЫНтНЯЖрЁЂDЁЊЗЧГЃСЫНтЁБЫФИіЕШМЖЃЌвРОнЯрЙиЪ§ОнЛцжЦГЩШчЯТСНЗљЭГМЦЭМЃЎ

ЃЈ1ЃЉетДЮЕїВщГщШЁСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉИљОнСНИіЭГМЦЭМЬсЙЉЕФаХЯЂЃЌВЙШЋетСНИіЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃга 3000 УћбЇЩњЃЌЧыФуЙРМЦШЋаЃЖдЁАЙиЕЦвЛаЁЪБЁБЗЧГЃСЫНтЕФбЇЩњгаЖрЩйУћЃП
ЁОД№АИЁПЃЈ1ЃЉетДЮЕїВщГщШЁСЫ50УћбЇЩњЃЛЃЈ2ЃЉЭММћНтЮіЃЛЃЈ3ЃЉЖдЁАЙиЕЦвЛаЁЪБЁБЗЧГЃСЫНтЕФбЇЩњга600Ућ.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩAЕФАйЗжБШМАШЫЪ§НјвЛВНМЦЫуГіД№АИМДПЩЃЛ
ЃЈ2ЃЉЯШЧѓГіBЕФШЫЪ§ЮЊЃЌДгЖјЕУГіDЕФШЫЪ§ЃЌШЛКѓНјвЛВНМЦЫуГіЭМжаШБЪЇЕФаХЯЂРДВЙШЋЭМаЮМДПЩЃЛ
ЃЈ3ЃЉгУЖдЁАЙиЕЦвЛаЁЪБЁБЗЧГЃСЫНтЕФбЇЩњеМЕФАйЗжБШГЫвдзмШЫЪ§МДПЩ.
ЃЈ1ЃЉ![]() ЃЈУћЃЉЃЌ
ЃЈУћЃЉЃЌ
Д№ЃКетДЮЕїВщГщШЁСЫ50УћбЇЩњЃЛ
ЃЈ2ЃЉBЕФШЫЪ§ЮЊЃК![]() ЃЈУћЃЉЃЌ
ЃЈУћЃЉЃЌ
DЕФШЫЪ§ЮЊЃК![]() ЃЈУћЃЉЃЌ
ЃЈУћЃЉЃЌ
CЫљеМЕФАйЗжБШЮЊЃК![]() ЃЌ
ЃЌ
DЫљеМЕФАйЗжБШЮЊЃК![]() ЃЌ
ЃЌ
ЁрВЙШЋЕФЭМаЮШчЯТЫљЪОЃК

ЃЈ3ЃЉ![]() ЃЈУћЃЉЃЌ
ЃЈУћЃЉЃЌ
Д№ЃКЖдЁАЙиЕЦвЛаЁЪБЁБЗЧГЃСЫНтЕФбЇЩњга600Ућ.


 аТЛюСІзмЖЏдБЪюЯЕСаД№АИ
аТЛюСІзмЖЏдБЪюЯЕСаД№АИ СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШєНЋзѓЭМе§ЗНаЮМєГЩЫФПщЃЌЧЁФмЦДГЩгвЭМЕФОиаЮЃЌЩшa=1ЃЌдђb=ЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
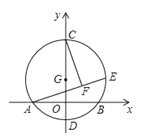
ЁОЬтФПЁПШчЭМЃЌвдG(0ЃЌ3)ЮЊдВаФЃЌАыОЖЮЊ6ЕФдВгыxжсНЛгкAЃЎBСНЕуЃЌгыyжсНЛгкCЃЌDСНЕуЃЌЕуEЮЊЁбGЩЯвЛЖЏЕуЃЌCFЁЭAEгкFЃЌЕуEдкЁбGЕФдЫЖЏЙ§ГЬжаЃЌЯпЖЮFGЕФГЄЖШЕФзюаЁжЕЮЊ(ЁЁЁЁ)
A.![]() 1B.2
1B.2![]() -2C.3
-2C.3![]() D.3
D.3![]() 3
3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
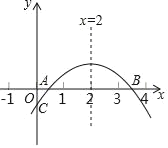
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсе§АыжсЯрНЛгкAЁЂBСНЕуЃЌгыyжсЯрНЛгкЕуCЃЌЖдГЦжсЮЊжБЯпxЃН2ЃЌЧвOAЃНOCЃЌдђЯТСаНсТлЃКЂйabcЃО0ЃЛЂк9a+3b+cЃМ0ЃЛЂлcЃОЉ1ЃЛЂмЙигкxЕФЗНГЬax2+bx+cЃН0ЃЈaЁй0ЃЉгавЛИіИљЮЊ1ЃЛЦфжае§ШЗЕФНсТлИіЪ§гаЃЈЁЁЁЁЃЉ
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМШ§НЧаЮABCЃЌBCЃН12ЃЌADЪЧBCБпЩЯЕФИпADЃН10ЃЎPЃЌNЗжБ№ЪЧABЃЌACБпЩЯЕФЕуЃЌQЃЌMЪЧBCЩЯЕФЕуЃЌСЌНгPQMNЃЌPNНЛADгкEЃЎЧѓ
ЃЈ1ЃЉШєЫФБпаЮPQMNЪЧОиаЮЃЌЧвPQЃКPNЃН1ЃК2ЃЎЧѓPQЁЂPNЕФГЄЃЛ
ЃЈ2ЃЉШєЫФБпаЮPQMNЪЧОиаЮЃЌЧѓЕБОиаЮPQMNУцЛ§зюДѓЪБЃЌЧѓзюДѓУцЛ§КЭPQЁЂPNЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧЬнаЮ AOBC жаЃЌACЁЮOBЃЌЧв OBЃН6ЃЌACЃН5ЃЌOAЃН4ЃЎ
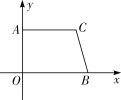
ЃЈ1ЃЉЧѓ BЁЂC СНЕуЕФзјБъЃЛ
ЃЈ2ЃЉвд OЁЂAЁЂBЁЂC жаЕФШ§ЕуЮЊЖЅЕуПЩзщГЩФФМИИіВЛЭЌЕФШ§НЧаЮЃП
ЃЈ3ЃЉЪЧЗёдкБп AC КЭ BC(КЌЖЫЕу)ЩЯЗжБ№ДцдкЕу M КЭЕу NЃЌЪЙЕУЁїMON ЕФУцЛ§зюДѓЪБЃЌЫќЕФжмГЄЛЙзюЖЬЃПШєДцдкЃЌЫЕУїРэгЩЃЌВЂЧѓГіетЪБЕу MЁЂN ЕФзјБъЃЛШєВЛДцдкЃЌЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
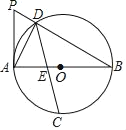
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌЧвABЃНmЃЈmЮЊГЃЪ§ЃЉЃЌЕуCЮЊ![]() ЕФжаЕуЃЌЕуDЮЊдВЩЯвЛЖЏЕуЃЌЙ§AЕузїЁбOЕФЧаЯпНЛBDЕФбгГЄЯпгкЕуPЃЌЯвCDНЛABгкЕуEЃЎ
ЕФжаЕуЃЌЕуDЮЊдВЩЯвЛЖЏЕуЃЌЙ§AЕузїЁбOЕФЧаЯпНЛBDЕФбгГЄЯпгкЕуPЃЌЯвCDНЛABгкЕуEЃЎ
ЃЈ1ЃЉЕБDCЁЭABЪБЃЌдђ![]() ЃНЁЁ ЁЁЃЛ
ЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЂйЕБЕуDдк![]() ЩЯвЦЖЏЪБЃЌЪдЬНОПЯпЖЮDAЃЌDBЃЌDCжЎМфЕФЪ§СПЙиЯЕЃЛВЂЫЕУїРэгЩЃЛ
ЩЯвЦЖЏЪБЃЌЪдЬНОПЯпЖЮDAЃЌDBЃЌDCжЎМфЕФЪ§СПЙиЯЕЃЛВЂЫЕУїРэгЩЃЛ
ЂкЩшCDГЄЮЊtЃЌЧѓЁїADBЕФУцЛ§SгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ФГЫўЙлЙтВуЕФзюЭтбиЕуEЮЊБФМЋЯюФПЕФЦ№ЬјЕу.вбжЊЕуEРыЫўЕФжажсЯпABЕФОрРыOEЮЊ10Уз,ЫўИпABЮЊ123Уз(ABДЙжБЕиУцBC),дкЕиУцCДІВтЕУЕуEЕФбіНЧІС=45Ёу,ДгЕуCбиCBЗНЯђЧАаа40УзЕНДяDЕу,дкDДІВтЕУЫўМтAЕФбіНЧІТ=60Ёу,ЧѓЕуEРыЕиУцЕФИпЖШEF.(НсЙћОЋШЗЕН0.1Уз)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy![]() x2bxcНЛxжсгкЕуAЃЌBЃЌЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЌгыyжсгкНЛгкЕуC(0ЃЌЉ2)ЃЎ
x2bxcНЛxжсгкЕуAЃЌBЃЌЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЌгыyжсгкНЛгкЕуC(0ЃЌЉ2)ЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЩЯШЁЕуDЃЌШєЕуDЕФКсзјБъЮЊ5ЃЌЧѓЕуDЕФзјБъМАЁЯADBЕФЖШЪ§ЃЛ
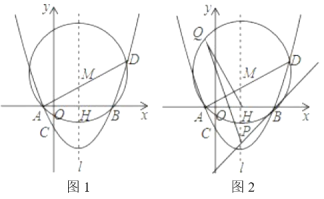
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшХзЮяЯпЖдГЦжс![]() НЛxжсгкЕуHЃЌЁїABDЕФЭтНгдВдВаФЮЊMЃЈШчЭМ1ЃЉЃЌ
НЛxжсгкЕуHЃЌЁїABDЕФЭтНгдВдВаФЮЊMЃЈШчЭМ1ЃЉЃЌ
ЂйЧѓЕуMЕФзјБъМАЁбMЕФАыОЖЃЛ
ЂкЙ§ЕуBзїЁбMЕФЧаЯпНЛ![]() гкЕуPЃЈШчЭМ2ЃЉЃЌЩшQЮЊЁбMЩЯвЛЖЏЕуЃЌдђдкЕуQдЫЖЏЙ§ГЬжа
гкЕуPЃЈШчЭМ2ЃЉЃЌЩшQЮЊЁбMЩЯвЛЖЏЕуЃЌдђдкЕуQдЫЖЏЙ§ГЬжа![]() ЕФжЕЪЧЗёБфЛЏЃПШєВЛБфЃЌЧѓГіЦфжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЪЧЗёБфЛЏЃПШєВЛБфЃЌЧѓГіЦфжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com