
����Ŀ��ij��˾�ɳ��׳�ǰ��ij���������ʱ����һ���������ͳ�����ͬʱ����������ͬһ����·��������ʻ���ٶȱ��ֲ��䣩��Ϊ��ȷ��������λ�ã�������OX��ʾ������·��ԭ��OΪ��ǧ��·�꣬��������Լ�����ٶ�Ϊ������ʾ�������������������ʻ���ٶ�Ϊ������ʾ����������ĸ�������ʻ���ٶ�Ϊ�㣬��ʾ������ֹ���г�Ϊ������ʾ����λ����ǧ���Ҳࣻ�г�Ϊ������ʾ����λ����ǧ����ࣻ�г�Ϊ�㣬��ʾ����λ����ǧ�״��������г̼�¼�����

����������е����ݣ�����������⣺
��1���׳�����7Сʱʱ��λ��Ϊ�� ��km���������ͳ�����λ��Ϊ�� ��km��
��2��������ͬʱ����xСʱʱ���׳�λ��Ϊ�� ��km���������ͳ�λ��Ϊ�� �� km ����x�Ĵ���ʽ��ʾ����
��3���׳�����ǰ����δ���ͣ�����������˾���ŷ������������ͽ�����ʻ3Сʱ���ʣ��׳�������ʻ3Сʱ���ܷ����̻���������ͳ��İ�������˵�����ɣ�
���𰸡���1����90����80��
��2��190��40x����80+50x��
��3���׳������̻���������ͳ��İ�����
�������������������1�����ݼ׳���λ�ú�ʱ������׳����ٶȣ�����ԭ����λ�ü�ȥ7Сʱ�Ժ��λ�ã���������׳�����7Сʱʱ��λ�ã�����5Сʱ��������λ�ú�7Сʱ��λ��������������ٶȣ��ٸ���·��=�ٶȡ�ʱ�䣬���ɵó��𰸣���2�����ݣ�1��������ٶȵó�xСʱ���·�̣�����ԭλ�ü�ȥ���ڵ�λ�ü��ɵó��׳���λ�ã��ã�1��������������ٶȳ���ʱ��������ڵ�λ�ã��ټ���������ԭ����λ�ü��ɵó��𰸣���3���ȼ��������3Сʱ�׳���λ�ú��������ͳ���λ�ã����߱Ƚϼ��ɵó��𰸣�
���������
��1����������ã�
�׳�����7Сʱʱ��λ��Ϊ��190-7����200��5��=-90��km����
�������ͳ�����λ��Ϊ��270-��270-170����2��7=-80��km����
�ʴ�Ϊ����90����80��
��2����������ã�
������ͬʱ����xСʱʱ���׳�λ��Ϊ��190��40x��
�������ͳ�λ��Ϊ����80+50x��
��3����x=3ʱ���׳�������λ���ǣ�190��40x=70��km����
�������ͳ���λ���ǣ���80+50x=70��km����
��׳������̻���������ͳ��İ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ȫһ���ĺ�30���ǵ�ֱ�����dz����ֱ������ABC����A��B��C�䣬�ֽ��������dz��ص���һ������ϳ�ֱ�DZߵ��е�ΪM�����е�Mת����������dz�ABC��ʹ��ֱ�Ƕ���Cǡ���������dz�A��B��C����б��A��B����������A��30�㣬AC��10ʱ����ֱ�Ƕ���C��C����ľ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������в���������ij�عرջ��ݽ����г����䶳��������������ij��˾�ڴ����ڼ�ɹ��䶳����60���������к�������֪�䶳�����ڳ�������ƽ��ÿ�������y1(��Ԫ)����������x(��)�Ĺ�ϵΪy1�� ����������ƽ��ÿ�������y2(��Ԫ)����������t(��)�Ĺ�ϵΪy2��
����������ƽ��ÿ�������y2(��Ԫ)����������t(��)�Ĺ�ϵΪy2��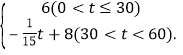
(1)t��x�Ĺ�ϵ�� ����y2ת��ΪxΪ�Ա����ĺ�������y2�� ��
(2)�贺���ڼ�����ȫ���䶳����ɻ��������W(��Ԫ)�����ڳ���������x(��)�ķ�Χ��0<x��20ʱ����W��x�Ĺ�ϵʽ(�������ڳ�������������������������)��
(3)�����㣬��20<x��30�ķ�Χ�ڣ����Ի������������������������������ʱx��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�Ƕ�֪����|5������2��|��ʾ5�멁2֮��ľ���ֵ��ʵ����Ҳ������Ϊ5�멁2����������������Ӧ������֮��ľ��룮������������������̽����
![]()
��1�������ϱ�ʾ5�멁2����֮��ľ������� ��
��2�������ϱ�ʾx��2������֮��ľ�����Ա�ʾΪ�� ����
��3��ͬ��|x+3|+|x��1|��ʾ������������x����Ӧ�ĵ㵽��3��1����Ӧ�ĵ�ľ���֮�ͣ������ҳ����з�������������x��ʹ��|x+3|+|x��1|=4���������������� ����
��4��������̽������|x+10|+|x+2|+|x��8|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ�
��5��������̽������|x+10|+|x+2|+|x��8|+|x��10|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬AB=4��tan��ACB=![]() ����D��E�ֱ���BC��AD���е㣬AF��BC��CE���ӳ����ڵ�F�����ı���AFBD�����Ϊ______��
����D��E�ֱ���BC��AD���е㣬AF��BC��CE���ӳ����ڵ�F�����ı���AFBD�����Ϊ______��
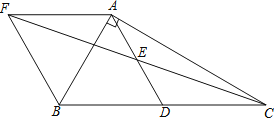
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ѿ���ֽƬABCD��EF�۵���ʹ��B���ڱ�AD�ϵĵ�B��������A���ڵ�A������
��1����֤��B��E=BF��
��2����AE=a��AB=b��BF=C���Բ���a��b��c֮���һ�ֹ�ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2�� ![]() x+cos��=0��������ȵ�ʵ�����������a���ڣ� ��
x+cos��=0��������ȵ�ʵ�����������a���ڣ� ��
A.0��
B.30��
C.45��
D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��PA������A��-1��0������P��1��2����ֱ��PB��һ�κ���y=-x+3��ͼ����
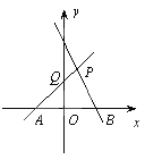
��1����ֱ��PA�ı���ʽ��Q������ꣻ
��2�����ı���PQOB�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com