
【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE. 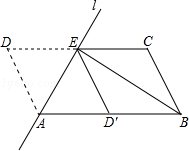
(1)求证:四边形BCED′是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2 .
【答案】
(1)证明:∵将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,
∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′,
∵四边形ABCD是平行四边形,
∴AB ![]() DC,
DC,
∴CE ![]() D′B,
D′B,
∴四边形BCED′是平行四边形;
(2)∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.

【解析】(1)利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形;(2)利用平行线的性质结合勾股定理得出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】三峡一期工程结束后的当年发电量为5.5×109度,某市有10万户居民,如果平均每户每年用电2.75×103度,那么三峡工程该年所发的电能供该市居民使用多少年?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) 
A.AB=BE
B.BE⊥DC
C.∠ADB=90°
D.CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把点(2,﹣3)先向右平移3个单位长度,再向上平移2个单位长度得到的点的坐标是( )
A.(5,﹣1)
B.(﹣1,﹣5)
C.(5,﹣5)
D.(﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F. 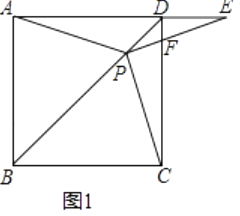
(1)证明:PC=PE;
(2)求∠CPE的度数;
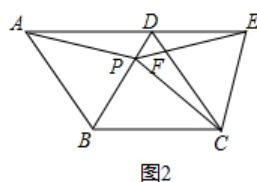
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB的长为a,延长线段AB至点C,使BC= ![]() .
. ![]()
(1)求线段AC的长(用含a的代数式表示);
(2)取线段AC的中点D,若DB=3,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
C. “明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com