
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯгаСНИіГЄЗНаЮ![]() КЭ
КЭ![]() ЃЌетСНИіГЄЗНаЮЕФПэЖМЪЧ2ИіЕЅЮЛГЄЖШЃЌГЄЗНаЮ
ЃЌетСНИіГЄЗНаЮЕФПэЖМЪЧ2ИіЕЅЮЛГЄЖШЃЌГЄЗНаЮ![]() ЕФГЄ
ЕФГЄ![]() ЪЧ4ИіЕЅЮЛГЄЖШЃЌГЄЗНаЮ
ЪЧ4ИіЕЅЮЛГЄЖШЃЌГЄЗНаЮ![]() ЕФГЄ
ЕФГЄ![]() ЪЧ8ИіЕЅЮЛГЄЖШЃЌЕу
ЪЧ8ИіЕЅЮЛГЄЖШЃЌЕу![]() дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ5ЃЌЧв
дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ5ЃЌЧв![]() СНЕужЎМфЕФОрРыЮЊ12ЃЎ
СНЕужЎМфЕФОрРыЮЊ12ЃЎ

ЃЈ1ЃЉЬюПе:Еу![]() дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ_________ ЃЌЕу
дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ_________ ЃЌЕу![]() дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ_________ЃЎ
дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ_________ЃЎ
ЃЈ2ЃЉШєЯпЖЮ![]() ЕФжаЕуЮЊ
ЕФжаЕуЮЊ![]() ЃЌЯпЖЮEHЩЯгавЛЕу
ЃЌЯпЖЮEHЩЯгавЛЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ ![]() вдУПУы4ИіЕЅЮЛЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌ
вдУПУы4ИіЕЅЮЛЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌ![]() вдУПУы3ИіЕЅЮЛЕФЫйЖШЯђзѓдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
вдУПУы3ИіЕЅЮЛЕФЫйЖШЯђзѓдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() УыЃЌЧѓЕБ
УыЃЌЧѓЕБ![]() ЖрЩйУыЪБЃЌ
ЖрЩйУыЪБЃЌ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШєГЄЗНаЮ![]() вдУПУы2ИіЕЅЮЛЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌГЄЗНаЮ
вдУПУы2ИіЕЅЮЛЕФЫйЖШЯђгвдШЫйдЫЖЏЃЌГЄЗНаЮ![]() ЙЬЖЈВЛЖЏЃЌЕБСНИіГЄЗНаЮжиЕўВПЗжЕФУцЛ§ЮЊ6ЪБЃЌЧѓГЄЗНаЮ
ЙЬЖЈВЛЖЏЃЌЕБСНИіГЄЗНаЮжиЕўВПЗжЕФУцЛ§ЮЊ6ЪБЃЌЧѓГЄЗНаЮ![]() дЫЖЏЕФЪБМфЃЎ
дЫЖЏЕФЪБМфЃЎ
ЁОД№АИЁПЃЈ1ЃЉ13ЃЌ11ЃЛЃЈ2ЃЉxЃН2ЛђxЃН![]() ЃЛЃЈ3ЃЉЕБГЄЗНаЮABCDдЫЖЏЕФЪБМф7.5УыЛђ8.5УыЪБЃЌжиЕўВПЗжЕФУцЛ§ЮЊ6ЃЎ
ЃЛЃЈ3ЃЉЕБГЄЗНаЮABCDдЫЖЏЕФЪБМф7.5УыЛђ8.5УыЪБЃЌжиЕўВПЗжЕФУцЛ§ЮЊ6ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЬѕМўПЩЯШЧѓГіЕуHБэЪОЕФЪ§ЮЊ13ЃЌШЛКѓдйНјвЛВНЧѓНтМДПЩЃЛ
ЃЈ2ЃЉИљОнЬтвтЯШЕУГіЕуMБэЪОЕФЪ§ЮЊЉ9ЃЌЕуNБэЪОЕФЪ§ЮЊ7ЃЌШЛКѓЗжЕБMЁЂNдкЕуOСНВрЛђЕБNЁЂMдкЕуOЭЌВрСНжжЧщПіНјвЛВНЗжЮіЬжТлМДПЩЃЛ
ЃЈ3ЃЉЩшГЄЗНаЮABCDдЫЖЏЕФЪБМфЮЊyУыЃЌЗжжиЕўВПЗжЮЊГЄЗНаЮEFCDЛђжиЕўВПЗжЮЊГЄЗНаЮCDHGСНжжЧщПіНјвЛВНЗжЮіЬжТлМДПЩ.
ЃЈ1ЃЉЁпГЄЗНаЮ![]() ЕФГЄ
ЕФГЄ![]() ЪЧ8ИіЕЅЮЛГЄЖШЃЌЕу
ЪЧ8ИіЕЅЮЛГЄЖШЃЌЕу![]() дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ5ЃЌ
дкЪ§жсЩЯБэЪОЕФЪ§ЪЧ5ЃЌ
ЁрЕуHБэЪОЕФЪ§ЮЊЃК![]() ЃЌ
ЃЌ
Ёп![]() СНЕужЎМфЕФОрРыЮЊ12ЃЌ
СНЕужЎМфЕФОрРыЮЊ12ЃЌ
ЁрЕуDБэЪОЕФЪ§ЮЊЃК![]() ЃЌ
ЃЌ
ЁпГЄЗНаЮ![]() ЕФГЄ
ЕФГЄ![]() ЪЧ4ИіЕЅЮЛГЄЖШЃЌ
ЪЧ4ИіЕЅЮЛГЄЖШЃЌ
ЁрЕуAБэЪОЕФЪ§ЮЊЃК![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЬтвтПЩжЊЃКЕуMБэЪОЕФЪ§ЮЊЉ9ЃЌЕуNБэЪОЕФЪ§ЮЊ7ЃЛЃЌОЙ§xУыКѓЃЌMЕуБэЪОЕФЪ§ЮЊЉ9+4xЃЌNЕуБэЪОЕФЪ§ЮЊ7Љ3xЃЛ
ЂйЕБMЁЂNдкЕуOСНВрЪБЃЌЕуOЮЊMЁЂNЕФжаЕуЃЌ
дђга![]() ЃЌ
ЃЌ
НтЕУxЃН2 ЃЛ
ЂкЕБNЁЂMдкЕуOЭЌВрЪБЃЌМДЕуNЁЂMЯргіЃЌ
дђга7Љ3xЃНЉ9+4x
НтЕУЃКxЃН![]()
злЩЯЃЌЕБxЃН2ЛђxЃН![]() ЪБЃЌOM=ON ЃЛ
ЪБЃЌOM=ON ЃЛ
ЃЈ3ЃЉЩшГЄЗНаЮABCDдЫЖЏЕФЪБМфyЮЊУыЃЌ
ЂйЕБжиЕўВПЗжЮЊГЄЗНаЮEFCDЪБЃЌ

DE=7+2y5= 2y12
Ёр 2(2y12) = 6ЃЌ
НтЕУЃКy = 7.5ЃЛ
ЂкЕБжиЕўВПЗжЮЊГЄЗНаЮCDHGЪБЃЌ

HD= 13 (7+2y) = 20 2yЃЌ
Ёр 2(202y) = 6ЃЌ
НтЕУЃКy =8.5ЃЛ
злЩЯЃЌЕБГЄЗНаЮABCDдЫЖЏЕФЪБМф7.5УыЛђ8.5УыЪБЃЌжиЕўВПЗжЕФУцЛ§ЮЊ6.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЫФБпаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌAB=6ЃЌBC=8ЃЌШєЁїAOBЪЧЕШбќШ§НЧаЮЃЌдђЦНааЫФБпаЮABCDЕФУцЛ§ЕШгк_______________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЕФЫФИіЖЅЕуЗжБ№дкЗДБШР§КЏЪ§![]() гы
гы![]() (xЃО0ЃЌ0ЃМmЃМn)ЕФЭМЯѓЩЯЃЌЖдНЧЯпBD//yжсЃЌЧвBDЁЭACгкЕуPЃЎвбжЊЕуBЕФКсзјБъЮЊ4ЃЎ
(xЃО0ЃЌ0ЃМmЃМn)ЕФЭМЯѓЩЯЃЌЖдНЧЯпBD//yжсЃЌЧвBDЁЭACгкЕуPЃЎвбжЊЕуBЕФКсзјБъЮЊ4ЃЎ
ЃЈ1ЃЉЕБm=4ЃЌn=20ЪБЃЎ
ЂйШєЕуPЕФзнзјБъЮЊ2ЃЌЧѓжБЯпABЕФКЏЪ§БэДяЪНЃЎ
ЂкШєЕуPЪЧBDЕФжаЕуЃЌЪдХаЖЯЫФБпаЮABCDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЫФБпаЮABCDФмЗёГЩЮЊе§ЗНаЮЃПШєФмЃЌЧѓДЫЪБmЃЌnжЎМфЕФЪ§СПЙиЯЕЃЛШєВЛФмЃЌЪдЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇОйАьдЫЖЏЛсЃЌдк1500УзЕФЯюФПжаЃЌВЮШќбЁЪждк200УзЕФЛЗаЮХмЕРЩЯНјааЃЌЯТЭММЧТМСЫХмЕУзюПьЕФвЛЮЛбЁЪжгызюТ§ЕФвЛЮЛбЁЪжЕФХмВНШЋЙ§ГЬЃЈСНШЫЖМХмЭъСЫШЋГЬЃЉЃЌЦфжаxДњБэЕФЪЧзюПьЕФбЁЪжШЋГЬЕФХмВНЪБМфЃЌyДњБэЕФЪЧетСНЮЛбЁЪжжЎМфЕФОрРыЃЌЯТСаЫЕВЛКЯРэЕФЪЧЃЈЃЉ
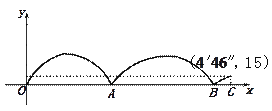
A. ГіЗЂКѓзюПьЕФбЁЪжгызюТ§ЕФбЁЪжЯргіСЫСНДЮЃЛ
B. ГіЗЂКѓзюПьЕФбЁЪжгызюТ§ЕФбЁЪжЕквЛДЮЯргіБШЕкЖўДЮЯргіЕФгУЪБЖЬЃЛ
C. зюПьЕФбЁЪжЕНДяжеЕуЪБЃЌзюТ§ЕФбЁЪжЛЙга415УзЮДХмЃЛ
D. ХмЕФзюТ§ЕФбЁЪжгУЪБ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊОиаЮABEDЃЌЕуCЪЧБпDEЕФжаЕуЃЌЧвAB=2AD.
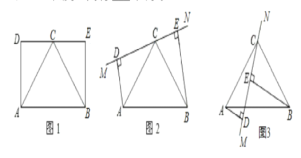
(1)гЩЭМ1ЭЈЙ§ЙлВьЁЂВТЯыПЩвдЕУЕНЯпЖЮACгыЯпЖЮBCЕФЪ§СПЙиЯЕЮЊ___ЃЌЮЛжУЙиЯЕЮЊ__ЃЛ
(2)БЃГжЭМ1жаЕФЁїABCЙЬЖЈВЛБф,ШЦЕуCа§зЊDEЫљдкЕФжБЯпMNЕНЭМ2жаЕФЮЛжУ(ЕБДЙЯпADЁЂBEдкжБЯпMNЕФЭЌВр).ЪдЬНОПЯпЖЮADЁЂBEЁЂDEГЄЖШжЎМфгаЪВУДЙиЯЕ?ВЂИјгшжЄУї(ЕквЛЮЪжаЕУЕНЕФВТЯыНсТлПЩвджБНгдкжЄУїжаЪЙгУ)ЃЛ
(3)БЃГжЭМ2жаЕФЁїABCЙЬЖЈВЛБф,МЬајШЦЕуCа§зЊDEЫљдкЕФжБЯпMNЕНЭМ3жаЕФЮЛжУ(ЕБДЙЯпЖЮADЁЂBEдкжБЯпMNЕФвьВр).ЪдЬНОПЯпЖЮADЁЂBEЁЂDEГЄЖШжЎМфга___ЙиЯЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
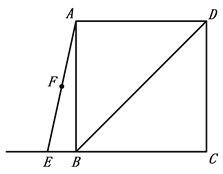
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌСЌНгBDЃЌЕуEЮЊCBБпЕФбгГЄЯпЩЯвЛЕуЃЌЕуFЪЧЯпЖЮAEЕФжаЕуЃЌЙ§ЕуFзїAEЕФДЙЯпНЛBDгкЕуM,СЌНгMEЁЂMC.
ЃЈ1ЃЉИљОнЬтвтВЙШЋЭМаЮЃЌВТЯы![]() гы
гы![]() ЕФЪ§СПЙиЯЕВЂжЄУїЃЛ
ЕФЪ§СПЙиЯЕВЂжЄУїЃЛ
ЃЈ2ЃЉСЌНгFBЃЌХаЖЯFB ЁЂFMжЎМфЕФЪ§СПЙиЯЕВЂжЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЕФФГдВЩЯЃЌгаЯвMNЃЌШЁMNЕФжаЕуPЃЌЮвУЧЙцЖЈ:ЕуPЕНФГЕуЃЈжБЯпЃЉЕФОрРыНазіЁАЯвжаОрЁБЃЌгУЗћКХЁА![]() ЁББэЪО.
ЁББэЪО.
ЯжЧыдквдWЃЈ-3ЃЌ0ЃЉЮЊдВаФЃЌАыОЖЮЊ2ЕФЁбWдВЩЯЃЌИљОнвдЯТЬѕМўНтД№ЫљЬсЮЪЬтЃК
ЃЈ1ЃЉвбжЊЯвMNГЄЖШЮЊ2.
ЂйШчЭМ1ЃКЕБMNЁЮxжсЪБЃЌжБНгаДГіЕНдЕуOЕФ![]() ЕФГЄЖШЃЛ
ЕФГЄЖШЃЛ
ЂкШчЙћMNдкдВЩЯдЫЖЏЪБЃЌдкЭМ2жаЛГіЪОвтЭМЃЌВЂжБНгаДГіЕНЕуOЕФ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЃЈ2ЃЉвбжЊЕу![]() ,ЕуNЮЊЁбWЩЯЕФвЛЖЏЕуЃЌгажБЯп
,ЕуNЮЊЁбWЩЯЕФвЛЖЏЕуЃЌгажБЯп![]() ЃЌЧѓЕНжБЯп
ЃЌЧѓЕНжБЯп![]() ЕФ
ЕФ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
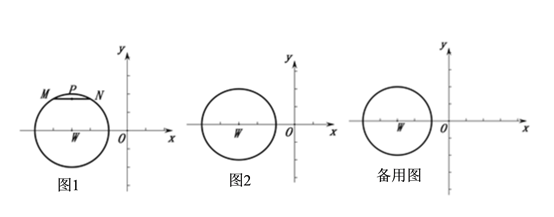
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉНтЗНГЬЃК
Ђй![]()
Ђк![]()
ЃЈ2ЃЉМЦЫуЃК
Ђй![]()
Ђк![]()
ЃЈ3ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйЧѓ![]() ЃЛ
ЃЛ
ЂкШє![]() ЃЌМЦЫу
ЃЌМЦЫу![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГаЁбЇЁАбнНВДѓШќЁБбЁАЮШќГѕШќжаЃЌМзЁЂввЁЂБћШ§ЮЛЦРЮЏЖдаЁбЁЪжЕФзлКЯБэЯжЃЌЗжБ№ИјГіЁАД§ЖЈЁБЃЈгУзжФИWБэЪОЃЉЛђЁАЭЈЙ§ЁБЃЈгУзжФИPБэЪОЃЉЕФНсТлЃЎ
ЂХЧыгУЪїзДЭМБэЪОГіШ§ЮЛЦРЮЏИјаЁбЁЪжчїчїЕФЫљгаПЩФмЕФНсТлЃЛ
ЂЦЖдгкаЁбЁЪжчїчїЃЌжЛгаМзЁЂввСНЮЛЦРЮЏИјГіЯрЭЌНсТлЕФИХТЪЪЧЖрЩйЃП
ЂЧБШШќЙцЖЈЃЌШ§ЮЛЦРЮЏжажСЩйгаСНЮЛИјГіЁАЭЈЙ§ЁБЕФНсТлЃЌдђаЁбЁЪжПЩШыЮЇНјШыИДШќЃЌЮЪчїчїНјШыИДШќЕФИХТЪЪЧ______________.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com