
【题目】观察下图回答问题: 
(1)指出小明的作业从哪一步开始出现的错误,请更正过来,并计算出正确结果;
(2)若a,b是不等式组 ![]() 的整数解(a<b),求上题{}分式的值.
的整数解(a<b),求上题{}分式的值.
【答案】
(1)解:小明第一步中括号内计算错了;
( ![]() ﹣1)÷
﹣1)÷ ![]()
=( ![]() ﹣
﹣ ![]() )×
)× ![]()
= ![]() ×
× ![]()
=a+b
(2)解: ![]()
∵解不等式①得:x>0,
解不等式②得:x<3,
∴不等式组的解集为0<x<3,
∵a,b是不等式组 ![]() 的整数解(a<b),
的整数解(a<b),
∴a=1,b=2,
∴原式=1+2=3
【解析】(1)先算括号内的减法,同时把除法变成乘法,再根据分式的乘法法则进行计算即可;(2)先求出不等式组的解集,求出a、b,最后代入求出即可.
【考点精析】本题主要考查了分式的混合运算和一元一次不等式组的整数解的相关知识点,需要掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】小刘上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小刘离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示,则下列说法不正确的是( )

A. 小刘家与超市相距3000米 B. 小刘去超市途中的速度是300米/分
C. 小刘在超市逗留了30分钟 D. 小刘从超市返回家比从家里去超市的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)![]() (2)(
(2)(![]() -
-![]() )×(-
)×(-![]() )
)
(3)![]() (4)(-2a2)3+ a8÷a2 +3a·a5
(4)(-2a2)3+ a8÷a2 +3a·a5
(5)(2x-5)(2x+5)-2x(2x-3) (6)(3x+y)2-(3x-y)2
查看答案和解析>>
科目:初中数学 来源: 题型:
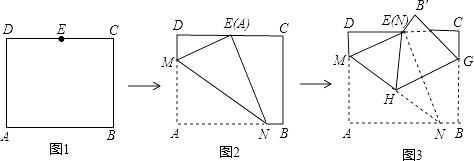
【题目】如图,在矩形ABCD中,AB=8 ![]() ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则下列结论正确的个数是( ) ①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG= ![]()
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B的坐标为(18,6).
(1)求直线l1,l2对应的函数表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,设点C的纵坐标为a,求点D的坐标(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图,是两车相距的路程d(千米)与行驶时间t(小时)的函数关系图象. 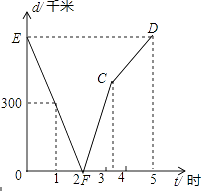
(1)A,B两城相距千米,经过小时两车相遇;
(2)分别求出甲、乙两车的速度;
(3)直接写出甲车距A城的路程S1、乙车距A城的路程S2与t的函数关系式;(不必写出t的范围)
(4)当两车相距100千米时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品20件和B种商品15件需380元;若购进A种商品15件和B种商品10件需280元.
(1)求A、B两种商品的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过900元,问最多能购进A种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
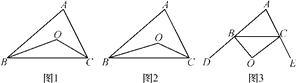
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com