
����Ŀ���������֣�
���ν���ǽ����ѧ�����һ����Ҫ��˼�뷽�����������ַ����ɽ��������ѧ֪ʶ���ֱ���������Ҿ��пɲ����ԣ��Ӷ����������ǿ��ٽ��⣮������ѧ���һЩ������ʽ���ܶ����ͨ����ʾ����ͼ������ķ�������ֱ���Ƶ��ͽ��ͣ�
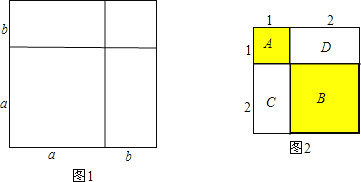
���磺����ͼ�εļ�������֤����ȫƽ����ʽ��
֤������һ���߳�Ϊa�������εı߳�����b���γ��������κ����������Σ���ͼ1��
���ͼ�ε�������Ա�ʾ�ɣ�
��a+b��2��a2+2ab+b2
�ࣨa+b��2 ��a2+2ab+b2
�����֤�������͵���ȫƽ����ʽ��
��Ƚ����
��1�����������������������ͼ�εļ�������֤��ƽ���ʽ����Ҫ��ͼ�β�д���������̣�
����������������ͼ�μ�������ķ���֤����13+23��32��
��ͼ2��A��ʾ1��1��1�������Σ�����1��1��1��13
B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ���ˣ�B��C��D�Ϳ��Ա�ʾ2��2��2�������Σ�����2��2��2��23��A��B��C��Dǡ�ÿ���ƴ��һ����1+2������1+2���Ĵ������Σ�
�ɴ˿ɵã�13+23����1+2��2��32
���Խ����
��2��������������Ƶ����̣�����ͼ�εļ�������ȷ����13+23+33���� ������Ҫ��д�����۲�����ͼ��д����֤���̣���
��3�������ع㣺
��������ı�ʾ����ͼ������ķ���̽����13+23+33+��+n3���� ������ֱ��д�����ۼ��ɣ�����д��������̣�
���𰸡���1������������2��62����֤���̼���������3��[![]() n��n+1��]2
n��n+1��]2
��������
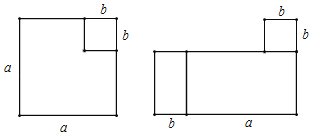
��1����Ƚ������ͼ���߳�Ϊa��b�����������Σ��߱���ƽ�У��Ӵ��������м�ȥС�����Σ�ʣ�µ�ͼ�ο��Էָ��2�������β�ƴ��һ�����Σ����ݵ�һ��ͼ�ε���Ӱ���ֵ������a2��b2���ڶ���ͼ�ε���Ӱ���ֵ�����ǣ�a+b����a��b����������֤ƽ���ʽ��
��2�����Խ������ͼ��A��ʾһ��1��1�������Σ�B��C��D��ʾ2��2��2�������Σ�E��F��G��ʾ3��3��3�������Σ���A��B��C��D��E��F��Gǡ�ÿ���ƴ��һ���߳�Ϊ��1+2+3���Ĵ������Σ����ݴ���������������ֱ�ʾ���������Եó�13+23+33��62��
��3�������ع㣺�������ʾ����ͼ�ε����̽��֪��13+23+33+��+n3����1+2+3+��+n��2����һ�����ɣ�
��1������ͼ����ͼ����Ӱ���ֵ������a2��b2��
��ͼ����Ӱ���ֵ�����ǣ�a+b����a��b����
��a2��b2����a+b����a��b����
�����֤��ƽ���ʽ��
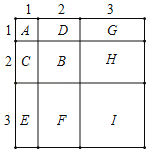
��2����ͼ��A��ʾ1��1��1�������Σ���1��1��1��13��
B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ�
��ˣ�B��C��D�Ϳ��Ա�ʾ2��2��2�������Σ�����2��2��2��23��
G��H��E��F��I���Ա�ʾ3��3��3�������Σ���3��3��3��33��
������ͼ��ǡ�ÿ���ƴ��һ����1+2+3������1+2+3���Ĵ������Σ�
�ɴ˿ɵã�13+23+33����1+2+3��2��62��
�ʴ�Ϊ��62��
��3���������ʾ����ͼ�ε����̽����֪��13+23+33+��+n3����1+2+3+��+n��2��
�֡�1+2+3+��+n��![]() n��n+1����
n��n+1����
��13+23+33+��+n3��[![]() n��n+1��]2��
n��n+1��]2��
�ʴ�Ϊ��[![]() n��n+1��]2��
n��n+1��]2��


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
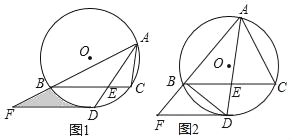
����Ŀ����ͼ1����ABC�ڽ�����O����BAC��ƽ���߽���O�ڵ�D����BC�ڵ�E��BE��EC������BD=2![]() ������D��DF��BC����AB���ӳ����ڵ�F��
������D��DF��BC����AB���ӳ����ڵ�F��
��1����֤��DFΪ��O�����ߣ�
��2������BAC=60����DE=![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������
��3����![]() ��DF+BF=8����ͼ2����BF�ij���
��DF+BF=8����ͼ2����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
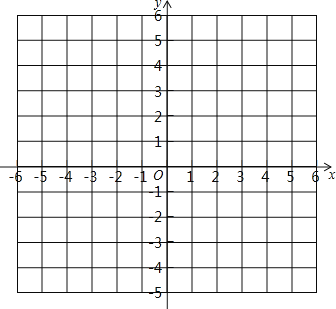
����Ŀ����֪��ƽ��ֱ������ϵ��������![]() ��
��![]() ��
��![]() ����ش��������⣺
����ش��������⣺
��1��������ϵ�������![]() ��λ�ã�
��λ�ã�
��2�������![]() �������������������
�������������������
��3����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ����Ϊ����������ε����Ϊ10�������ڣ���ֱ��д����
����Ϊ����������ε����Ϊ10�������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
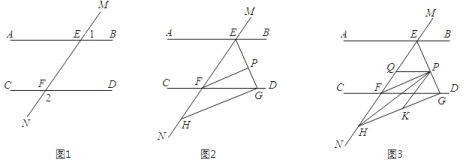
����Ŀ����ͼ 1��ֱ�� MN ��ֱ�� AB��CD �ֱ��ڵ� E��F����1 ���2 ������
(1)���ж�ֱ�� AB ��ֱ�� CD ��λ�ù�ϵ����˵�����ɣ�
(2)��ͼ 2����BEF ���EFD �Ľ�ƽ���߽��ڵ� P��EP �� CD ���ڵ� G���� H �� MN ��һ�㣬��GH��EG����֤��PF��GH��
(3)��ͼ 3����(2)�������£����� PH���� GH ��ȡһ�� K��ʹ�á�PKG=2��HPK������ P �� PQ ƽ�֡�EPK �� EF �ڵ� Q���ʡ�HPQ �Ĵ�С�Ƿ����仯�������䣬�������ֵ�����仯��˵�����ɣ�(��ܰ��ʾ�������ε������ڽǺ�Ϊ 180��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB=�� ����PD=�� ����
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=6����DAB=60����AE�ֱ�BC��BD�ڵ�E��F��CE=2������CF�����½��ۣ��١�ABF�ա�CBF���ڵ�E��AB�ľ�����2![]() ����tan��DCF=
����tan��DCF=![]() ���ܡ�ABF�����Ϊ
���ܡ�ABF�����Ϊ![]() ������һ���������м�����������
������һ���������м�����������
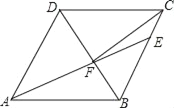
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�����߶�����ȵ������Σ���O�͵�P������������ڲ����㣮
��1����ͼ�٣������P����������������ڽ�ƽ���ߵĽ��㣬��ô��BPC�͡�BAC��������������ϵ����˵�����ɣ�
��2����ͼ�ڣ������O��������������ߴ�ֱƽ���ߵĽ��㣬��ô��BOC�͡�BAC��������������ϵ����˵�����ɣ�
��3����ͼ�ۣ������P�������������ڽ�ƽ���ߵĽ��㣩����O�����������ߴ�ֱƽ���ߵĽ��㣩ͬʱ�ڲ��ȱߡ�ABC���ڲ�����ô��BPC�͡�BOC��������������ϵ����ֱ�ӻش�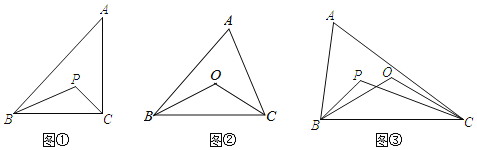
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
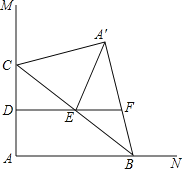
����Ŀ����ͼ����MAN=90������C�ڱ�AM�ϣ�AC=4����BΪ��AN��һ���㣬����BC����A��BC����ABC����BC����ֱ�߶Գƣ���D��E�ֱ�ΪAC��BC���е㣬����DE���ӳ���A��B����ֱ���ڵ�F������A��E������A��EFΪֱ��������ʱ��AB�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com