
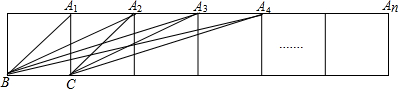
分析 作CH⊥BA4于H,根据正方形的性质、勾股定理以及三角形的面积公式求出CH、A4H,根据正切的概念求出tan∠BA4C,总结规律解答.
解答 解: 作CH⊥BA4于H,
作CH⊥BA4于H,
由勾股定理得,BA4=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,A4C=$\sqrt{10}$,
△BA4C的面积=4-2-$\frac{3}{2}$=$\frac{1}{2}$,
∴$\frac{1}{2}$×$\sqrt{17}$×CH=$\frac{1}{2}$,
解得,CH=$\frac{\sqrt{17}}{17}$,
则A4H=$\sqrt{{A}_{4}{C}^{2}-C{H}^{2}}$=$\frac{13\sqrt{17}}{17}$,
∴tan∠BA4C=$\frac{CH}{{A}_{4}H}$=$\frac{1}{13}$,
1=12-1+1,
3=22-2+1,
7=32-3+1,
∴tan∠BAnC=$\frac{1}{{n}^{2}-n+1}$,
故答案为:$\frac{1}{13}$;$\frac{1}{{n}^{2}-n+1}$.
点评 本题考查的是正方形的性质、勾股定理的应用以及正切的概念,掌握正方形的性质、熟记锐角三角函数的概念是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
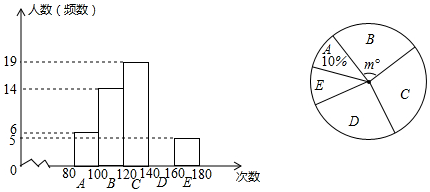
 国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com