
����Ŀ�����壺��ͼ��1�������ֱ��ԡ�ABC������AC��BC��ABΪ���������������������ACDE��BCFG��ABMN�����������������Ϊ��ABC����չ��Ҷ�����Σ�������������������Ϊ��ABC����չ˫Ҷ�����Σ� 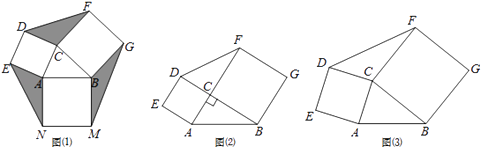
��1������ABC����չ˫Ҷ������ACDE��BCFG���ǡ�ABC����DCF������ֱ�ΪS1��S2 �� ����ͼ��2��������ACB=90��ʱ����֤��S1=S2 ��
����ͼ��3��������ACB��90��ʱ��S1��S2�Ƿ���Ȼ��ȣ���˵�����ɣ�
��2����֪��ABC�У�AC=3��BC=4��������չ��Ҷ�����Σ��ǡ�DCF����AEN����BGM�������ΪS��������ͼ��1��̽��������ACB�Ķ��������仯ʱ��S��ֵ�Ƿ����仯�������䣬���S��ֵ�����仯�����S�����ֵ��
���𰸡�
��1��֤������ͼ1��
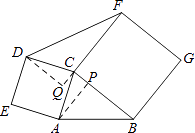
��������ACDE��������BCFG��
��AC=DC��BC=FC����ACD=��BCF=90�㣬
�ߡ�ACB=90�㣬���DCF=90�㣬
���ACB=��DCF=90�㣮
�ڡ�ABC�͡�DFC�У�
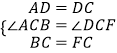 ��
��
���ABC�ա�DFC��SAS����
��S��ABC=S��DFC��
��S1=S2
��S1=S2���������£�
�⣺��ͼ3������A��AP��BC�ڵ�P������D��DQ��FC��FC���ӳ����ڵ�Q��
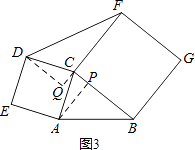
���APC=��DQC=90�㣮
���ı���ACDE��BCFG��Ϊ�����Σ�
��AC=CD��BC=CF��
�ߡ�ACP+��ACQ=90�㣬��DCQ+��ACQ=90�㣮
���ACP=��DCQ��
�ڡ�APC�͡�DQC��
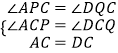 ��
��
���APC�ա�DQC��AAS����
��AP=DQ��
��BC��AP=DQ��FC��
�� ![]() BC��AP=
BC��AP= ![]() DQ��FC
DQ��FC
��S1= ![]() BC��AP��S2=
BC��AP��S2= ![]() FC��DQ��
FC��DQ��
��S1=S2
��2���ɣ�2���ã�S�ǡ�ABC�����������
ҪʹS���ֻ��������ABC��������
�൱��ABC��ֱ�������Σ�����ACB=90��ʱ��S�����ֵ��
��ʱ��S=3S��ABC=3�� ![]() ��3��4=18
��3��4=18
����������1���������ε����ʿ��Եó�AC=DC��BC=FC����ACB=��DCF=90�㣬�Ϳ��Եó���ABC�ա�DFC���ó����ۣ���2����ͼ3������A��AP��BC�ڵ�P������D��DQ��FC��FC���ӳ����ڵ�Q��ͨ��֤����APC�ա�DQC����DQ=AP���ó����ۣ���3����ͼ 1�����ݣ�2�����Եó�S=3S��ABC �� ҪʹS���ҪʹS��ABC�����AVB=90��ʱS��ABC��Ϳ���������ۣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
��֪��Ϊʲô�κ�����ѭ��С��������д�ɷ�����ʽ������Ľ����̻������ԭ��ͷ�����
��1���Ķ����в��ϣ�
���⣺����һԪһ�η��̽�![]() ���ɷ�����
���ɷ�����
�� ![]() ��
��
��![]() ����֪
����֪![]() ��
��
�� ![]() ����������Ὣ�������߶�����10�����ã�
����������Ὣ�������߶�����10�����ã�
�ɽ�� ![]() ����
���� ![]() ��
��
��գ���![]() ֱ��д�ɷ�����ʽΪ_____________ ��
ֱ��д�ɷ�����ʽΪ_____________ ��
��2�����������������С��![]() ���ɷ�����Ҫ��д������һԪһ�η��̽��н��Ĺ���.
���ɷ�����Ҫ��д������һԪһ�η��̽��н��Ĺ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABCD��ƽ���ı��Σ�AEƽ�֡�BAD��CFƽ�֡�BCD���ֱ�BC��AD��E��F����֤��AF=EC�� 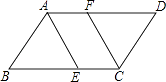
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
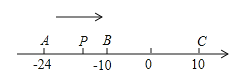
����Ŀ����֪��������A��B��C���������ֱ��ʾ��������24����10��10������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ�����PA= ��PC= ��
��2������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�������������ͬ�����ٶȷ������˶����յ�A��
�����˶���������tΪ��ֵʱP��Q�غϣ�
���ڵ�Q��ʼ�˶�����P��Q����֮��ľ����ܷ�Ϊ2����λ����������������ʱ��P��ʾ�����������������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������OABC�����Ϊ9,��OΪ����ԭ��,��B�ں���y=![]() ��k>0,x>0����ͼ���ϵ�P��m,n���Ǻ���ͼ��������һ��,����P�ֱ���x��y��Ĵ���,����ֱ�ΪE,F.�������OEPF��������OABC���غϵIJ��ֵ����ΪS.
��k>0,x>0����ͼ���ϵ�P��m,n���Ǻ���ͼ��������һ��,����P�ֱ���x��y��Ĵ���,����ֱ�ΪE,F.�������OEPF��������OABC���غϵIJ��ֵ����ΪS.
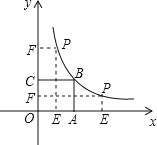
(1)��k��ֵ��
(2)��S=![]() ʱ ��p������ꣻ
ʱ ��p������ꣻ
(3)д��S����m�Ĺ�ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A��B��C��D�ĸ������㣨���������ʾ����������3AB=BC=2CD����A��D��������ʾ�����ֱ��ǩ�6��5�����߶�AC���е�����ʾ�����ǣ�������
![]()
A. ��3 B. ��1 C. 3 D. ��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ô���ʽ��ʾ��x��2����Y�IJ��ƽ��������ȷ���ǣ� ��
A. (2x-y)2B. 2(x-y)2C. 2x-y2D. (x-2y)2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y����a��1��x2��x+a2��1ͼ��ԭ�㣬��a��ȡֵΪ��������
A.a����1B.a��1C.a����1D.��ȷ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com