

���� ��1������ȫ�������Σ���ȫ�������ζ�Ӧ�߶�֮�����ȹ�ϵ�������D����E�����ꣻ
��2�����ô���ϵ������������ߵĽ���ʽ��
��3����Ϊ��s�ı���ʽ����Ҫʶ�������Σ��������ߣ����˶����̣������ε�ƽ�ƣ��ӿ�ʼ���������ܹ���ʱ$\frac{3}{2}$�룬�ڼ���Ի��ֳ������Σ���0��t��$\frac{1}{2}$ʱ����Ӧͼa����$\frac{1}{2}$��t��1ʱ����Ӧͼb����1��t��$\frac{3}{2}$ʱ����Ӧͼc��
�ڵ��˶�ֹͣʱ����E����y�ᣬ��E��-3��2���˶�����E�䣨0��$\frac{7}{2}$������֪������BCDE��y�������صõ��߶ε��е��˶���·�߳�ΪCE'�ij�����������������ƽ����3����λ������ƽ����$\frac{3}{2}$����λ���ɴ˵õ�ƽ��֮��������߽���ʽ����������䶥�����꣮
��� 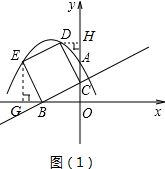 �⣺��1���������֪��OB=2��OC=1��
�⣺��1���������֪��OB=2��OC=1��
��ͼ��1����ʾ����D����DH��y����H����E����EG��x����G��
��֤��CDH�ա�BCO��
��DH=OC=1��CH=OB=2��
��D��-1��3����
ͬ���ɵá�EBG�ա�BCO��
��BG=OC=1��EG=OB=2��
��E��-3��2����
�ʴ�Ϊ����-1��3������-3��2����
��2�������߾�����0��2������-1��3������-3��2����
��$\left\{\begin{array}{l}{c=2}\\{a-b+c=3}\\{9a-3b+c=2}\end{array}\right.$��
��� $\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$��
��y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2��
��3���ٵ���D�˶���y����ʱ��t=$\frac{1}{2}$��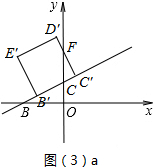
��0��t��$\frac{1}{2}$ʱ����ͼ��3��a��ʾ��
��D��C�佻y���ڵ�F��
��tan��BCO=$\frac{OB}{OC}$=2��
�֡ߡ�BCO=��FCC�䣬
��tan��FCC��=2����$\frac{FC'}{CC'}$=2��
��CC��=$\sqrt{5}$t��
��FC��=2$\sqrt{5}$t��?
��S��CC��F?=$\frac{1}{2}$CC��•FC��=$\frac{1}{2}$$\sqrt{5}$t��2$\sqrt{5}$t=5t2
����B�˶�����Cʱ��t=1��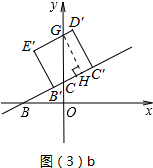
��$\frac{1}{2}$��t��1ʱ����ͼ��3��b��ʾ��
��D��E�佻y���ڵ�G����G��GH��B��C����H��
��Rt��BOC��BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��
��GH=$\sqrt{5}$��
��CH=$\frac{1}{2}$GH=$\frac{1}{2}$$\sqrt{5}$��
��CC��=$\sqrt{5}$t��
��HC��=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$��
��GD��=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$��
��S����CC��D��G?=$\frac{1}{2}$��$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$+$\sqrt{5}$t�� $\sqrt{5}$=5t-$\frac{5}{4}$��
����E�˶���y����ʱ��t=$\frac{3}{2}$��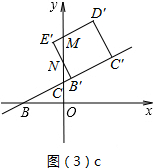
��1��t��$\frac{3}{2}$ʱ����ͼ��3��c��ʾ��
��D��E�䡢E��B��ֱ�y���ڵ�M��N��
��CC��=$\sqrt{5}$t��B��C��=$\sqrt{5}$��
��CB��=$\sqrt{5}$t-$\sqrt{5}$��
��B��N=2CB��=2$\sqrt{5}$t-2$\sqrt{5}$��
��B��E��=$\sqrt{5}$��
��E��N=B��E��-B��N=3$\sqrt{5}$-2$\sqrt{5}$t��
��E��M=$\frac{1}{2}$E��N=$\frac{1}{2}$��3$\sqrt{5}$-2$\sqrt{5}$t����
��S��MNE��=$\frac{1}{2}$��3$\sqrt{5}$-2$\sqrt{5}$t��•$\frac{1}{2}$��3$\sqrt{5}$-2$\sqrt{5}$t��=5t2-15t+$\frac{45}{4}$��
��S�����B��C��D��MN?=S������B��C��D��E��?-S��MNE��?=$��\sqrt{5}��^{2}$-��5t2-15t+$\frac{45}{4}$��=-5t2+15t-$\frac{25}{4}$��
����������S��x�ĺ�����ϵʽΪ��
��0��t��$\frac{1}{2}$ʱ��S=5t2��
��$\frac{1}{2}$��t��1ʱ��S=5t-$\frac{5}{4}$��
��1��t��$\frac{3}{2}$ʱ��S=-5t2+15t-$\frac{25}{4}$��
�ڵ���E�˶�����E��ʱ���˶�ֹͣ����ͼ��3��d��ʾ��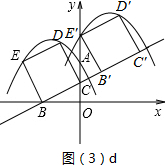
������BCDE��y�������صõ��߶ε��е��˶���·�߳�ΪCE'�ij���
�ߡ�CB��E��=��BOC=90�㣬��BCO=��B��CE�䣬
���BOC�ס�E��B��C��
��$\frac{OB}{B'E'}$=$\frac{BC}{E'C}$��
��OB=2��B��E��=BC=$\sqrt{5}$��
��$\frac{2}{\sqrt{5}}$=$\frac{\sqrt{5}}{E'C}$��
��CE��=$\frac{5}{2}$����������BCDE��y�������صõ��߶ε��е��˶���·�߳�Ϊ$\frac{5}{2}$��
��OE��=OC+CE��=1+$\frac{5}{2}$=$\frac{7}{2}$��
��E�䣨0��$\frac{7}{2}$����
�ɵ�E��-3��2���˶�����E�䣨0��$\frac{7}{2}$������֪��������������ƽ����3����λ������ƽ����$\frac{3}{2}$����λ��
��y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=-$\frac{1}{2}$��x+$\frac{3}{2}$��2+$\frac{25}{8}$��
��ԭ�����߶�������Ϊ��-$\frac{3}{2}$��$\frac{25}{8}$����
���˶�ֹͣʱ�������ߵĶ�������Ϊ��$\frac{3}{2}$��$\frac{37}{8}$����
�ʴ�Ϊ��$\frac{5}{2}$����$\frac{3}{2}$��$\frac{37}{8}$����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˶��κ�����ͼ�������ʡ�����ϵ���������ʽ���������뼸�α任��ƽ�ƣ������������ε��ж������ʡ�ȫ�������ε��ж������ʡ������ε����ʵȵ��ۺ�Ӧ�ã��ѵ����ڵڣ�3���ʣ�ʶ�������κ�������ƽ�ƹ��̵IJ�ͬ���ǽ������Ĺؼ����ڣ�


 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д� ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b3+a3=2b6 | B�� | ��-3pq��2=-9p2q2 | C�� | 5y3+3y5=15y8 | D�� | b9��b3=b3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
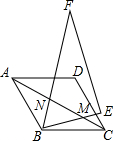 ��ͼ���߳�Ϊ2������ABCD�У���BAD=60�㣬���С�BFE=30������ǰ��BEF������BEF��B��ת�á�BE��F�䣬BE�䣬BF������ֱ�߷ֱ��߶�AC�ڵ�M��N������C����ֱ��BE��ĶԳƵ�ΪC�䣬��C��N��ACʱ��AN�ij�Ϊ$\sqrt{3}$-1��
��ͼ���߳�Ϊ2������ABCD�У���BAD=60�㣬���С�BFE=30������ǰ��BEF������BEF��B��ת�á�BE��F�䣬BE�䣬BF������ֱ�߷ֱ��߶�AC�ڵ�M��N������C����ֱ��BE��ĶԳƵ�ΪC�䣬��C��N��ACʱ��AN�ij�Ϊ$\sqrt{3}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -a2b+2a2b=a2b | B�� | 3a-a=a | C�� | 2a3+3a2=5a5 | D�� | 3a+2a=5a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڱ߳�Ϊ10��������ABCD�У�AC�ǶԽ��ߣ���E��G�ֱ��DZ�BC��CD�ϵĵ㣬����ABE��AE�۵��õ���AFE����Fǡ�����ڶԽ���AC�ϣ�ͬ������CEG��GE�۵��õ���HEG��ʹ��EH��EF�غϣ�����AH��DH��
��ͼ��ʾ���ڱ߳�Ϊ10��������ABCD�У�AC�ǶԽ��ߣ���E��G�ֱ��DZ�BC��CD�ϵĵ㣬����ABE��AE�۵��õ���AFE����Fǡ�����ڶԽ���AC�ϣ�ͬ������CEG��GE�۵��õ���HEG��ʹ��EH��EF�غϣ�����AH��DH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
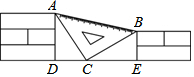 �μ䣬С��������ʦ�ĵ���ֱ�����ǰ��棬��С�ĵ�����ǽ֮�䣨��ͼ������ACB=90�㣬AC=BC�������ǰ�Ŀ̶ȿ�֪AB=20cm��С�Ϻܿ��֪������ǽש��ĺ�ȵ�ƽ����ÿ��ש�ĺ����ȣ�Ϊ$\frac{200}{13}$cm��
�μ䣬С��������ʦ�ĵ���ֱ�����ǰ��棬��С�ĵ�����ǽ֮�䣨��ͼ������ACB=90�㣬AC=BC�������ǰ�Ŀ̶ȿ�֪AB=20cm��С�Ϻܿ��֪������ǽש��ĺ�ȵ�ƽ����ÿ��ש�ĺ����ȣ�Ϊ$\frac{200}{13}$cm���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com