练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （本题满分9分）
    “知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技比赛．下图为
    我市某校2011年参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图：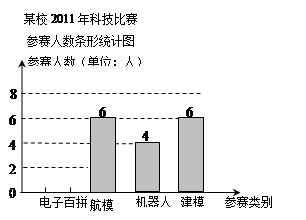


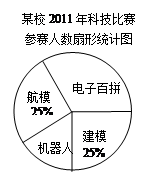
    （1）该校参加机器人、建模比赛的人数分别是       人和        人；
    （2）该校参加科技比赛的总人数是              人，电子百拼所在扇形的圆心角的度数是               °，并把条形统计图补充完整；
    （3）从全市中小学参加科技比赛选手中随机抽取80人，其中有32人获奖. 2011年我市中小学参加科技比赛人数共有2485人，请你估算2011年参加科技比赛的获奖人数约是多少人?


    解：答：（1） 4      6       ……………………………………………………2分
    （2） 24      120   （4分） 图略（6分）
    （3）2485×=994   ………………………………………………………………9分

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （本题满分12分）

    已知直线（＜0）分别交轴、轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作轴的垂线交直线AB于点C，设运动时间为秒．

    （1）当时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．

    ① 直接写出＝1秒时C、Q两点的坐标；

    ② 若以Q、C、A为顶点的三角形与△AOB相似，求的值．

    （2）当时，设以C为顶点的抛物线与直线AB的另一交点为D

    （如图2），① 求CD的长；

    ② 设△COD的OC边上的高为，当为何值时，的值最大？

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题满分10分）
    已知：如图，矩形DEFG的一边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，AH是边BC上的高，AH与GF相交于点K，已知BC=12，AH=6，EF∶GF=1∶2，求矩形DEFG的周长．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年陕西省兴平市九年级上学期期末练习数学卷 题型：解答题

    （本题满分12分）

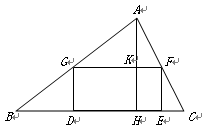
     已知菱形ABCD的边长为1．∠ADC=60°，等边△AEF两边分别交边DC、CB于点E、F。

    1.（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；

    2.（2）若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．

    ①猜想验证：如图2．猜想△AEF的外心P落在哪一直线上，并加以证明；

    ②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断是否为定值．若是．请求出该定值；若不是．请说明理由。

     

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年苏州市区九年级上学期期末考试数学卷 题型：填空题

    （本题满分8分）已知P（－3，m）和Q(1，m)是抛物线y＝2x2＋bx＋1上的两点．

     1.(1)求b的值；

     2.(2)判断关于x的一元二次方程2x2＋bx＋1＝0是否有实数根，若有，求出它的实数根；若没有，请说明理由；

    3. (3)将抛物线y＝2x2＋bx＋1的图象向上平移k(k是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值．

     

    查看答案和解析>>

    科目：初中数学 来源：2011-2012年江苏省扬州市九年级第一学期期末考试数学卷 题型：解答题

    （本题满分10分）已知a、b满足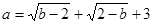

    1.（1）求a、b的值；

    2.（2）求二次函数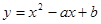图象与x轴交点坐标；

    3.（3）写出（2）中，当y>0时，x的取值范围。

     

    查看答案和解析>>

    同步练习册答案