
【题目】已知数轴上A,B两点对应的数分别为-2和8,P为数轴上一点,对应的数为x.
(1)线段PA的长度可表示为_________(用含![]() 的式子表示);
的式子表示);
(2)在数轴上是否存在点P,使得PA-PB=6?若存在,求出x的值;若不存在,请说明理由;
(3)当P为线段AB的中点时,点A,B,P同时开始在数轴上分别以每秒3个单位长度,每秒2个单位长度,每秒1个单位长度沿数轴正方向运动,试问经过几秒,PB=2PA?
【答案】(1)![]() ;(2)存在,当
;(2)存在,当![]() 时,PA-PB=6;(3)经过1秒或5秒,PB=2PA.
时,PA-PB=6;(3)经过1秒或5秒,PB=2PA.
【解析】
(1)根据数轴上两点间的距离公式可得结果;
(2)分别表示出PA和PB建立绝对值方程,根据x的取值范围去掉绝对值解方程即可;
(3)设运动时间为t秒,根据速度关系可求出A点追上P点,A点追上B点的时刻,再分别讨论不同位置时,利用PB=2PA建立方程求解.
解:(1)∵A点对应的数为-2,P点对应的数为x
∴PA=![]()
故答案为:![]() ;
;
(2)存在点P使得PA-PB=6,理由如下:
∵A点对应的数为8,P点对应的数为x
∴PB=![]()
∵PA-PB=6
![]()
①当![]() 时,方程变形为
时,方程变形为![]()
此时方程无解;
②当![]() 时,方程变形为
时,方程变形为![]()
解得![]() ;
;
③当![]() 时,方程变形为
时,方程变形为![]()
此时方程无解;
综上所述,当![]() 时,PA-PB=6.
时,PA-PB=6.
(3)设运动时间为t秒,
∵P点为AB的中点,
∴P点对应的数为![]() ,PA=PB=
,PA=PB=![]()
A点追上P点时,有![]() ,解得
,解得![]()
A点追上B点时,有![]() ,解得
,解得![]()
t秒时,A点对应的数为![]() ,P点对应的数为
,P点对应的数为![]() ,B点对应的数为
,B点对应的数为![]()
①当![]() 时,数轴上从左到右依次为:A,P,B,
时,数轴上从左到右依次为:A,P,B,
PB=![]() ,PA=
,PA=![]()
由PB=2PA可得:![]() ,解得
,解得![]() ;
;
②当![]() 时,A,P重合,PB≠2PA;
时,A,P重合,PB≠2PA;
③当![]() 时,数轴上从左到右依次为:P,A,B,
时,数轴上从左到右依次为:P,A,B,
PB=![]() ,PA=
,PA=![]()
由PB=2PA可得![]() ,解得
,解得![]() ;
;
④当![]() 时,A,B重合,PB≠2PA;
时,A,B重合,PB≠2PA;
⑤当![]() 时,数轴上从左到右依次为:P,B,A,
时,数轴上从左到右依次为:P,B,A,
PB=![]() ,PA=
,PA=![]()
由PB=2PA可得![]() ,解得
,解得![]() (舍去);
(舍去);
综上所述,经过1秒或5秒时,PB=2PA.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平行四边形ABCD 中, A 的角平分线交CD 于 E .
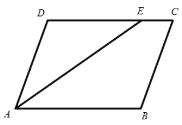
(1)若B 110,求AED 的度数;
(2)若 DE : EC 3 :1, AB 的长为8 ,求 AD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
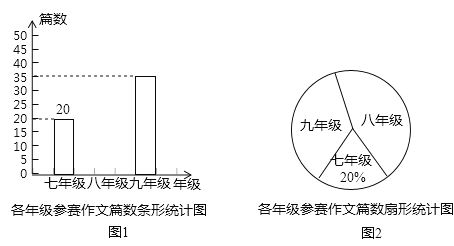
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
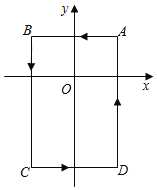
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
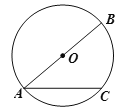
【题目】如图,AC是以AB为直径的⊙O的弦,点D是⊙O上的一点,过点D作⊙O的切线交直线AC于点E,AD平分∠BAE,若AB=10,DE=3,则AE的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
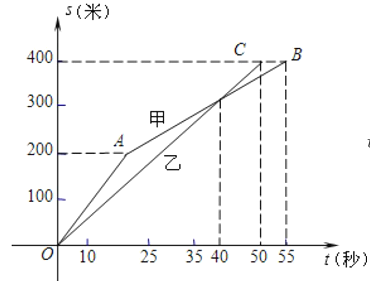
【题目】如图,在甲、乙两名同学进行400米跑步比赛中,路程S(米)与时间(t)之间的函数关系的图像分别为折线OAB和线段OC请根据图上信息回答下列问题
(1) 先到达终点;
(2)第 秒时, 追上 ;
(3)比赛过程中, 的速度适中保持不变;
(4)优胜者在比赛过程中所跑的路程S(米)关于时间t(秒)的函数解析式及定义域为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
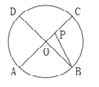
【题目】如图,A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿OC→![]() →DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为
→DO的路线做匀速运动,当点P运动到圆心O时立即停止.设运动时间为![]() (s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
(s),∠APB的度数为y度,则下列图象中表示y(度)与 t(s)之间的函数关系最恰当的是 ( )
A. 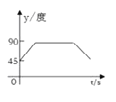 B.
B. 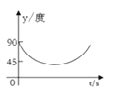 C.
C. 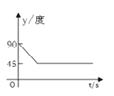 D.
D. 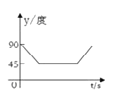
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com