
【题目】如图,已知四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,CE⊥AD,E为垂足.求证:AB+AD=2AE.

【答案】证明见解析.
【解析】
过点C作CH⊥AB,交AB的延长线于点H.利用角平分线性质得CH=CE,∠HCA=∠ECA,证△ACH≌△ACE(AAS),得AH=AE.∠HBC=∠D.再证△BHC≌△DEC(AAS),得HB=DE,
所以AB+AD=AB+AE+DE=AB+AE+HB=AH+AE=2AE.
证明:如图,过点C作CH⊥AB,交AB的延长线于点H.

∵AC平分∠BAD,CE⊥AD,
∴CH=CE,∠HCA=∠ECA(等角的余角相等).
在△ACH和△ACE中,
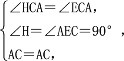
∴△ACH≌△ACE(AAS),
∴AH=AE.
又∵∠ABC+∠HBC=180°,
∠ABC+∠D=180°,
∴∠HBC=∠D.
在△BHC和△DEC中,
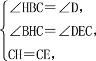
∴△BHC≌△DEC(AAS),
∴HB=DE,
∴AB+AD=AB+AE+DE=AB+AE+HB=AH+AE=2AE.


科目:初中数学 来源: 题型:
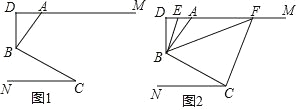
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
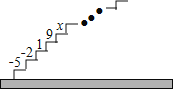
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.
尝试 (1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出点A′,B′,C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
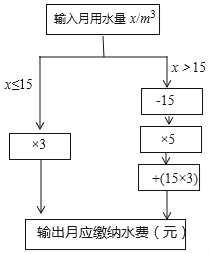
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=x2+2x﹣3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(﹣4,0),与y轴交于点D(0,2).
(1)求抛物线C2的解析式;
(2)设点P为线段AB上一动点(点P不与点A,B重合),过点P作x轴的垂线交抛物线C1于点M,交抛物线C2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.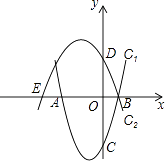
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( ) 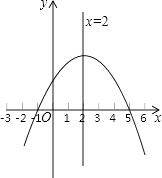
A.ac<0
B.a﹣b+c>0
C.b=﹣4a
D.关于x的方程ax2+bx+c=0的根是x1=﹣1,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2﹣x﹣3.
(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象; 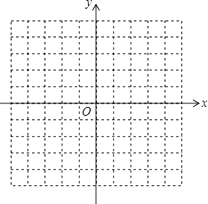
(2)根据图象直接回答:当x为何值时,y<0?当x为何值时y>﹣3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:

(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com