
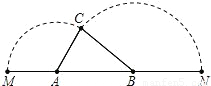
 ,满足1<x<2.
,满足1<x<2. ,满足1<x<2.
,满足1<x<2. 或
或 .
.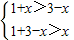 ,
,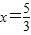 ,满足1<x<2,
,满足1<x<2,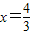 ,满足1<x<2,
,满足1<x<2,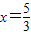 或
或 ;
;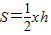 ,
, ,
,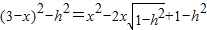 ,
, ,
,
 x2h2=-2x2+6x-4=-2(x-
x2h2=-2x2+6x-4=-2(x- )2+
)2+ (
( ≤x<2),
≤x<2), 时(满足
时(满足 ≤x<2)S2取最大值
≤x<2)S2取最大值 ,从而S取最大值
,从而S取最大值 ;
; ,
, x2h2=-2x2+6x-4
x2h2=-2x2+6x-4 )2+
)2+ (1<x≤
(1<x≤ ),
),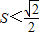 ,
,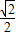 .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
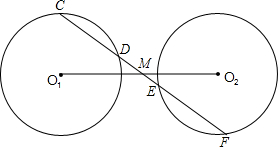 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
18、如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知P、Q是△ABC的边BC上的两点,BQ=CP,若不增加任何字母与辅助线,要使△ABP≌△ACQ,则还需增加一个条件是
如图,已知P、Q是△ABC的边BC上的两点,BQ=CP,若不增加任何字母与辅助线,要使△ABP≌△ACQ,则还需增加一个条件是查看答案和解析>>
科目:初中数学 来源: 题型:
 几何基础问题
几何基础问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com