


 -1
-1 +1
+1 ,解方程组
,解方程组 ,求出A点坐标.根据勾股定理求出OA、BC的长度,易求梯形AOBC的高,从而求出梯形AOBC的面积.△OBE是等腰直角三角形,腰长是2,易求其面积.
,求出A点坐标.根据勾股定理求出OA、BC的长度,易求梯形AOBC的高,从而求出梯形AOBC的面积.△OBE是等腰直角三角形,腰长是2,易求其面积. 解:因为AO∥BC,上底边OA在直线y=x上,
解:因为AO∥BC,上底边OA在直线y=x上, ,
, ,
, ,x=-
,x=- (负值舍去).
(负值舍去).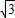 .
. ,
, ),
), =
= ,
, =3
=3 ,
, ,
, ,
, ,
, ×(3
×(3 +
+ )×
)× =3+
=3+ ,
, ×2×2=2,
×2×2=2, -2=1+
-2=1+ .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
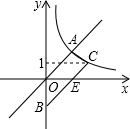 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为( )
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为( )| A、3 | ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),则四边形AOEC的面积为| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |

查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(57):20.7 反比例函数的图象、性质和应用(解析版) 题型:选择题


 -1
-1 +1
+1查看答案和解析>>
科目:初中数学 来源:第30章《反比例函数》中考题集(06):30.2 反比例函数的图像和性质(解析版) 题型:选择题


 -1
-1 +1
+1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com