
小明在家中利用物理知识称量某个品牌纯牛奶的净含量,称得六盒纯牛奶的含量分别为:248mL,250mL,249mL,251mL,249mL,253mL,对于这组数据,下列说法正确的是( ).
A.平均数为251mL B.中位数为249mL
C.众数为250mL D.方差为
科目:初中数学 来源:2016届江西吉安二中等九校中考一模数学试卷(解析版) 题型:解答题
?ABCD中,点E在AD上,DE=CD,请仅用无刻度的直尺,按要求作图(保留作图痕迹,不写作法)
(1)在图1中,画出∠C的角平分线;
(2)在图2中,画出∠A的角平分线.
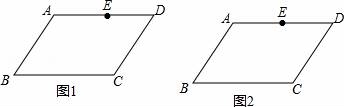
查看答案和解析>>
科目:初中数学 来源:2016届江西吉安二中等九校中考一模数学试卷(解析版) 题型:计算题
如图,⊙O的弦AB与半径OC相交于点P,BC∥OA,∠C=50°,那么∠APC的度数为 .

查看答案和解析>>
科目:初中数学 来源:2016届江西省景德镇市中考二模数学试卷(解析版) 题型:解答题
【特例发现】如图1,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.求证:EP=FQ.
【延伸拓展】如图2,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作Rt△ABE和Rt△ACF,射线GA交EF于点H.若AB=kAE,AC=kAF,请思考HE与HF之间的数量关系,并直接写出你的结论.
【深入探究】如图3,在△ABC中,G是BC边上任意一点,以A为顶点,向△ABC外作任意△ABE和△ACF,射线GA交EF于点H.若∠EAB=∠AGB,∠FAC=∠AGC,AB=kAE,AC=kAF,上一问的结论还成立吗?并证明你的结论.
【应用推广】在上一问的条件下,设大小恒定的角∠IHJ分别与△AEF的两边AE、AF分别交于点M、N,若△ABC为腰长等于4的等腰三角形,其中∠BAC=120°,且∠IHJ=∠AGB=θ=60°,k=2;
求证:当∠IHJ在旋转过程中,△EMH、△HMN和△FNH均相似,并直接写出线段MN的最小值(请在答题卡的备用图中补全作图).

查看答案和解析>>
科目:初中数学 来源:2016届江西省景德镇市中考二模数学试卷(解析版) 题型:解答题
如图甲,在两平行线l1,l2上各任取两个点A、C与B、D,则有S△ABD=S△CBD.请选用这条性质仅使用直尺在下列网络图上解决下面问题:图1,2的网格是由若干块单位正方形构成的,其中A、B、C、E均为格点.
如图1,过点C作直线把△ABC分成面积相等的两部分,并将该直线与AB边的交点标作D,保留作图痕迹;
如图2,过点E作直线把△ABC分成面积相等的两部分,并将该直线与BC边的交点标作F,保留作图痕迹.

查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:解答题
如图,抛物线 经过点A(1,0)和点B(5,0),与y轴交于点C.
经过点A(1,0)和点B(5,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)以点A为圆心,作与直线BC相切的⊙A,请判断⊙A与y轴有怎样的位置关系,并说明理由;
(3)在直线BC上方的抛物线上任取一点P,连接PB、PC,请问:△PBC的面积是否存在最大值?若存在,求出这个值和此时点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(贵州铜仁卷)数学(解析版) 题型:填空题
太和殿(明朝称为奉天殿、黄极殿),俗称“金銮殿”,面积为2377.00m2,用科学记数法表示这个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com