
【题目】已知:如图,Rt△ABC中,∠ABC=90°,AD平分∠BAC交BC于D.
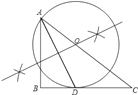
(1)用尺规作⊙O,使⊙O过A、D两点,且圆心O在AC上.(保留作图痕迹,不写作法)
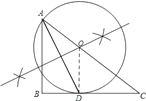
(2)求证:BC与⊙O相切;
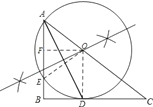
(3)设圆O交AB于点E,若AE=2,CD=2BD.求线段BE的长和弧DE的长.

【答案】(1)作图见解析; (2)证明见解析;(3)BE=1, ![]() 的长度为
的长度为![]() .
.
【解析】试题分析:(1)根据题意得:O点应该是AD垂直平分线与AC的交点;由此作AD的垂直平分线与AC交点即为圆心,然后以OA为半径即可作圆;
(2))由∠BAC的角平分线AD交BC边于D,与圆的性质可证得AB∥OD,又由∠B=90°,则问题得证;
(3)连接OE,过点O作OF⊥AB于点F,
由垂径定理定理以及△AOF与△ACB相似推导得出AB的长,从而得BE的长,由OD∥AB可得△OCD∽△ACB,从而得出△AOE是等边三角形,进而推得∠EOD=60°,从而可得![]() 的长度.
的长度.
试题解析:(1)如图所示,⊙O即为所求:
(2)连接OD,
∵OA=OD,∴∠OAD=∠ODA,
∵AD平分∠BAC,∴∠BAD=∠OAD,
∴∠BAD=∠ODA,∴OD∥AB,
∴∠ODC=∠ABC=90°,
∵OD是半径,
∴BC与⊙O相切;
(3)连接OE,过点O作OF⊥AB于点F,
∵AE=2,∴由垂径定理定理可知:AF=1,
∵CD=2BD,∴ ![]() ,
, ![]() ,
,
∵OF∥BC,∴△AOF∽△ACB,
∴![]() ,
,
∵OF=BD,∴ ![]()
![]() ,
,
∴![]() ,∴AB=3,
,∴AB=3,
∴BE=AB-AE=1,
∵OD∥AB,∴△OCD∽△ACB,∴ ![]() ,
,
∴OD=2,∴OA=OD=AE,
∴△AOE是等边三角形,
∴∠AEO=60°,∵OD∥AB,∴∠EOD=60°,
∴![]() 的长度为
的长度为![]() =
= ![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
【题目】某儿童服装店欲购进A、B两种型号的儿童服装;经调查:B型号童装的进货单价是A型号童装的进货单价的两倍,购进A型号童装60件和B型号童装40件共用去2100元.
求A、B两种型号童装的进货单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为方便顾客停车,决定设计一个地下停车场,为了测得该校地下停车场的限高CD,在施工时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 面积相等的两个三角形全等
B. 全等三角形的面积一定相等
C. 形状相同的两个三角形全等
D. 两个等边三角形一定全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾已经成为时下最普遍与敏感的话题.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
级别 | 观 点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |

请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 %;
(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com