

���� ��1�����ݸ��ʹ�ʽ���ɵã�
��2��������״ͼչʾ12�ֵȿ��ܵĽ���������ݹ��������ж�ֻ��A��Ƭ�ϵ����������ǹ���������ɴ�12�ֵȿ��ܵĽ�������ҳ��鵽�����ſ�Ƭ�ϵ������ǹ������Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
��� �⣺��1���μ������ȡһ�ſ�Ƭ������4�ֵȿ��ܽ�������г鵽�Ŀ�Ƭ�ϵ����ǹ������Ľ����3�֣�
���Լμγ�ȡһ�ſ�Ƭ�ϵ����ǹ������ĸ���P1=$\frac{3}{4}$��
��2�������
| A | B | C | D | |
| A | ��A��B�� | ��A��C�� | ��A��D�� | |
| B | ��B��A�� | ��B��C�� | ��B��D�� | |
| C | ��C��A�� | ��C��B�� | ��C��D�� | |
| D | ��D��A�� | ��D��B�� | ��D��C�� |
���� ���⿼�����б�������״ͼ���������б�������״ͼ��չʾ���п��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��������ʣ�Ҳ�����˹�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
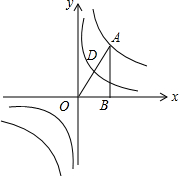 ��ͼ������������y=$\frac{8}{x}$��ͼ��ֱ��������OAB�Ķ���A��DΪб��OA���е㣬�����D�ķ����������Ľ���ʽΪy=$\frac{2}{x}$��
��ͼ������������y=$\frac{8}{x}$��ͼ��ֱ��������OAB�Ķ���A��DΪб��OA���е㣬�����D�ķ����������Ľ���ʽΪy=$\frac{2}{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
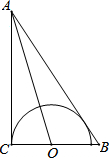 ��ͼ����Rt��ABC�У���ACB=90�㣬��BAC�Ľ�ƽ���߽�BC�ڵ�O��OC=2���Ե�OΪԲ��OCΪ�뾶��Բ��
��ͼ����Rt��ABC�У���ACB=90�㣬��BAC�Ľ�ƽ���߽�BC�ڵ�O��OC=2���Ե�OΪԲ��OCΪ�뾶��Բ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
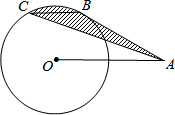 ��ͼ��A�ǰ뾶Ϊ2�ġ�O���һ�㣬OA=4��AB�С�O�ڵ�B����BC��OA������AC����ͼ����Ӱ���ֵ����Ϊ$\frac{2}{3}$�У�
��ͼ��A�ǰ뾶Ϊ2�ġ�O���һ�㣬OA=4��AB�С�O�ڵ�B����BC��OA������AC����ͼ����Ӱ���ֵ����Ϊ$\frac{2}{3}$�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com