
| A. | 扩大了一倍 | B. | 扩大了两倍 | C. | 扩大了四倍 | D. | 没有变化 |
分析 根据题意可以求得n边形的每个内角的度数,从而可以表示出正n边形的边长与半径,从而可以求得正n边形的边长与半径之比.
解答 解:设正n边形的边长为x,
则正n边形的每个中心角是$\frac{360°}{n}$,
∴正n边形的半径是:$\frac{\frac{x}{2}}{sin\frac{180°}{n}}$,
∴正n边形的边长与半径之比是:$\frac{x}{\frac{\frac{x}{2}}{sin\frac{180°}{n}}}$=2sin$\frac{180°}{n}$,
∴圆的半径扩大一倍,正n边形的边长与半径之比不变,
故选D.
点评 本题考查正多边形和圆,锐角三角函数,解直角三角形等知识,解题的关键是明确题意,找出所求问题需要的条件.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
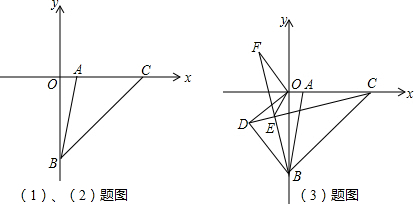
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
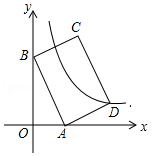 如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$的图象经过点D,则k值为( )
如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=$\frac{k}{x}$的图象经过点D,则k值为( )| A. | -14 | B. | 14 | C. | 7 | D. | -7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
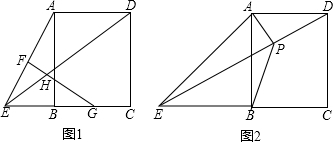
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com