
【题目】如图,矩形ABCD中,AB=8,AD=5,点E![]() 为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.
为DC边上一个动点,把△ADE沿AE折叠,点D的对应点D’落在矩形ABCD的对称轴上时,DE的长为____________.

【答案】![]() 或
或![]()
【解析】分析:过点D′作MN⊥AB于点N,MN交CD于点M,由矩形有两条对称轴可知要分两种情况考虑,根据对称轴的性质以及折叠的特性可找出各边的关系,在直角△EMD′与△AND′中,利用勾股定理可得出关于DM长度的一元二次方程,解方程即可得出结论.
详解:过点D′作MN⊥AB于点N,MN交CD于点M,如图1、所示.
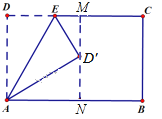
设DE=a,则D′E=a.
∵矩形ABCD有两条对称轴,
∴分两种情况考虑:
①当DM=CM时,
AN=DM=![]() CD=
CD=![]() AB=4,AD=AD′=5,
AB=4,AD=AD′=5,
由勾股定理可知:
ND′=![]() ,
,
∴MD′=MN-ND′=AD-ND′=2,EM=DM-DE=4-a,
∵ED′2=EM2+MD′2,即a2=(4-a)2+4,
解得:a=![]() ;
;
②当MD′=ND′时,
MD′=ND′=![]() MN=
MN=![]() AD=
AD=![]() ,
,
由勾股定理可知:
AN=![]() ,
,
∴EM=DM-DE=AN-DE=![]() -a,
-a,
∵ED′2=EM2+MD′2,即a2=(![]() a)2+(
a)2+(![]() )2,
)2,
解得:a=![]() .
.
综上知:DE=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() ..
..


科目:初中数学 来源: 题型:
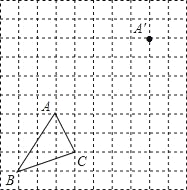
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC进行平移,得到△A′B′C′,使点A与A′对应,请在网格中画出△A′B′C′;
(2)线段AA′与线段CC′的位置关系是: ;(填“平行”或“相交”)
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx-5的图象经过点A(2,-1).
(1)求k的值;
(2)画出这个函数的图象;
(3)若将此函数的图象向上平移m个单位后与坐标轴围成的三角形的面积为1,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式
(1)﹣(﹣5)﹣(+7)
(2)|﹣5﹣8|+24÷(﹣3)
(3)﹣0.25÷(﹣![]() )×(1﹣
)×(1﹣![]() )
)
(4)36×(![]() )
)
(5)1÷[![]() ﹣(﹣1+1
﹣(﹣1+1![]() )]×4
)]×4
(6)23﹣(1﹣0.5)×![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y与x的关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售利润最大?
(3)若限定商店最多购进A型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com