练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．计算：$\sqrt{5}$（$\sqrt{5}$+$\frac{1}{\sqrt{5}}$）+$\root{3}{-64}$-|-$\sqrt{81}$|-$\sqrt{1\frac{9}{16}}$．

    分析 原式利用二次根式性质，平方根、立方根定义，以及绝对值的代数意义计算即可得到结果．

    解答 解：原式=5+1-4-9-$\frac{5}{4}$=-$\frac{33}{4}$．

    点评 此题考查了实数的运算，平方根、立方根，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．【阅读理解】我们知道，当a＞0且b＞0时，（$\sqrt{a}$-$\sqrt{b}$）2≥0，所以a-2$\sqrt{ab}$+≥0，从而a+b≥2$\sqrt{ab}$（当a=b时取等号），
    【获得结论】设函数y=x+$\frac{a}{x}$（a＞0，x＞0），由上述结论可知：当x=$\frac{a}{x}$即x=$\sqrt{a}$时，函数y有最小值为2$\sqrt{a}$
    【直接应用】（1）若y1=x（x＞0）与y2=$\frac{1}{x}$（x＞0），则当x=1时，y1+y2取得最小值为2．
    【变形应用】（2）若y1=x+1（x＞-1）与y2=（x+1）2+4（x＞-1），则$\frac{{y}_{2}}{{y}_{1}}$的最小值是4
    【探索应用】（3）在平面直角坐标系中，点A（-3，0），点B（0，-2），点P是函数y=$\frac{6}{x}$在第一象限内图象上的一个动点，过P点作PC⊥x轴于点C，PD⊥y轴于点D，设点P的横坐标为x，四边形ABCD的面积为S
    ①求S与x之间的函数关系式；
    ②求S的最小值，判断取得最小值时的四边形ABCD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

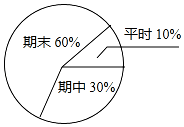    6．下面的表格是李刚同学一学期数学成绩的记录，根据表格提供的信息回答下面的问题 
    考试类别                  平时期中考试期末考试
    第一单元第二单元第三单元第四单元
    成绩888690929096
    （1）李刚同学6次成绩众数是90．
    （2）李刚同学6次成绩的中位数是90．
    （3）李刚同学平时成绩的平均数是89．
    （4）如果用下图的权重给李刚打分，他应该得多少分？（满分100分，写出解题过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知a，b都是实数，且（12a+b）2+|3a-b-5|=0，求13a2-b的平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

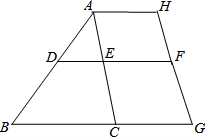    10．如图：已知∠DAE=55°，∠ADE=60°，∠ACB=65°，∠H与∠G互补，试说明AH∥DF的理由．
    解：因为∠DAE+∠ADE+∠AED=180°（三角形内角和等于180°），
    又∠DAE=55°，∠ADE=60°（已知），
    所以∠AED=65°（等式性质）．
    因为∠ACB=65°（已知），
    所以∠ACB=∠AED（等量代换），
    所以DF∥BG（同位角相等，两直线平行），
    因为∠H与∠G互补（已知），
    所以∠H+∠G=180°，
    所以AH∥BG（同旁内角互补，两直线平行），
    所以AH∥DF（如果两条直线都与第三条直线平行，那么这两条直线平行）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，函数y=kx与y=$\frac{m}{x}$的图象在第一象限内交于点A，过点A作AD垂直x轴于点D，且S△AOD=$\frac{3}{2}$．
    （1）求反比例函数的关系式；
    （2）若AD=1，试求k的值；
    （3）若kx-$\frac{m}{x}$＞0，请直接写出x的取值范围-3＜x＜0或x＞3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．化简：$\sqrt{50}$-$\sqrt{72}$=-$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，矩形ABCD中，AB=7cm，AD=4cm，点E为AD上一定点，F为AD延长线上一点，且DF=acm，点P从A点出发，沿AB边向点B以2cm/s的速度运动，运动到B点停止，连结PE，设点P运动的时间为ts，△PAE的面积为ycm2，当0≤t≤1时，△PAE的面积y（cm2）关于时间t（s）的函数图象如图2所示，连结PF，交CD于点H．
    （1）t的取值范围为0≤t≤3.5，AE=1cm；
    （2）如图3，将△HDF沿线段DF进行翻折，与CD的延长线交于点M，连结AM，当a为何值时，四边形PAMH为菱形？
    （3）在（2）的条件下求出点P的运动时间t．

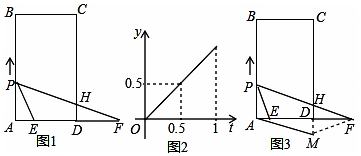
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知$\sqrt{x-2}$+$\sqrt{y+5}$=0，则x=2，y=-5．

    查看答案和解析>>

    同步练习册答案