
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 型号 | 占地面积(m2/个) | 使用农户数(户/个) | 造价(万元/个) |
| A | 15 | 18 | 2 |
| B | 20 | 30 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
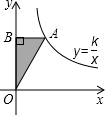 如图,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥y轴,垂足为点B,S△AOB=3,则以下结论:
如图,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥y轴,垂足为点B,S△AOB=3,则以下结论:| A. | ①② | B. | ③④ | C. | ②④ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
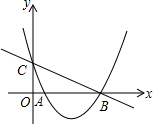 如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )| A. | y=-$\frac{3}{x}$ | B. | y=$\frac{3}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=-$\frac{6}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 85.5分 | B. | 90分 | C. | 92分 | D. | 265分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com