
【题目】如图,Rt△ABC中,∠C=90°,AC=24,点D在边BC上, CD=10,BD=26.点P是线段AD上一动点,当半径为12的⊙P与△ABC的一边相切时,AP的长为_____.
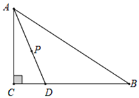
【答案】![]() 或
或![]()
【解析】
根据勾股定理得到AB=![]() =12
=12![]() ,AD=
,AD=![]() =26,当⊙P于BC相切时,点P到BC的距离=12,过P作PH⊥BC于H,则PH=12,当⊙P于AB相切时,点P到AB的距离=12,根据相似三角形的性质即可得到结论.
=26,当⊙P于BC相切时,点P到BC的距离=12,过P作PH⊥BC于H,则PH=12,当⊙P于AB相切时,点P到AB的距离=12,根据相似三角形的性质即可得到结论.
∵在Rt△ABC中,∠C=90°,AC=24,BD+CD=36,
∴AB=![]() =12
=12![]() ,
,
在Rt△ADC中,∠C=90°,AC=24,CD=10,
∴AD=![]() =26,
=26,
当⊙P于BC相切时,点P到BC的距离=12,
过P作PH⊥BC于H
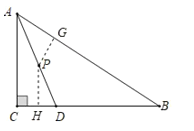
则PH=12,
∵∠C=90°,
∴AC⊥BC,
∴PH∥AC,
∴△DPH∽△DAC,
∴![]() ,
,
∴![]() ,
,
∴PD=13,
∴AP=13;
当⊙P于AB相切时,点P到AB的距离=12,
过P作PG⊥AB于G,
则PG=12,
∵AD=BD=26,
∴∠PAG=∠B,
∵∠AGP=∠C=90°,
∴△AGP∽△BCA,
∴![]() ,
,
∴![]() ,
,
∴AP=![]() ,
,
∵CD=10<12,
∴半径为6的⊙P不与△ABC的AC边相切,
综上所述,AP的长为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=![]() ,DE=3.
,DE=3.

求:(1)⊙O的半径;(2)弦AC的长;(3)阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度,2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2013年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2013年底共建设了多少万平方米廉租房.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:四边形ABCD中,AD∥BC,∠ADC=90°,AD=4,CD=2,BC=5,点E在BC边上自B向C运动(不与点C重合),连接AE,过点E作AE的垂线交直线CD于F点.设BE的长为![]() ,CF的长为
,CF的长为![]() .
.
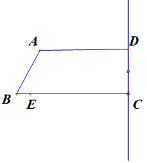
(1) 求![]() 的值
的值
(2) 求![]() 的长,(用含
的长,(用含![]() 的代数式表示)
的代数式表示)
(3) 连接AF,在点E运动的过程中,△![]() 的外心
的外心![]() 点的位置也随之变化,探索:
点的位置也随之变化,探索:![]() 满足什么条件,外心
满足什么条件,外心![]() 落在四边形ABCD的边上或形外.
落在四边形ABCD的边上或形外.
查看答案和解析>>
科目:初中数学 来源: 题型:
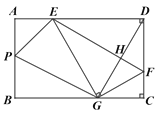
【题目】如图,在矩形ABCD中,点E,F分别在边AD,DC上,AB=6,DF=4,将矩形沿直线EF折叠,点D恰好落在BC边上的点G处,连接DG交EF于点H.
(1)求DE的长度.
(2)求![]() 的值.
的值.
(3)若AB边上有且只存在2个点P,使△APE与△BPG相似,请直接写出边AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字![]() ,
,![]() ,
,![]() ,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求这张卡片上的数字为偶数的概率;
(2)随机地抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数恰好为“![]() ”的概率是多少?
”的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com