
【题目】在Rt△ABC与Rt△ABD中,![]() ,
,![]() ,AC、BD相交于点G,过点A作
,AC、BD相交于点G,过点A作![]() 交CB的延长线于点E,过点B作
交CB的延长线于点E,过点B作![]() 交DA的延长线于点F,AE、BF相交于点H.
交DA的延长线于点F,AE、BF相交于点H.
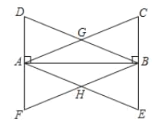
(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°.

(1)求∠BCD的度数;
(2)将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() 两点间的距离表示为
两点间的距离表示为![]() .且
.且![]() .
.
(1)数轴上表示2和5的两点之间的距离是___,
数轴上表示2和5的两点之间的距离是___,
数轴上表示1和3的两点之间的距离是___;
(2)数轴上表示x和1的两点A和B之间的距离是___,如果|AB|=2,那么x=___;
(3)当代数式|x+1|+|x2|取最小值时,相应x的取值范围是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
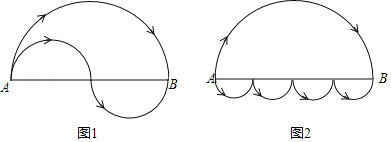
【题目】黑蚂蚁沿着大半圆从A地爬到B地,白蚂蚁沿着两个小半圆弧路线也从A地爬到B地.它们同时从A地出发,让人奇怪的是,两只蚂蚁同时爬到B地.假设AB=a
(1)请你帮忙裁决,两只蚂蚁谁爬得快?
(2)两只蚂蚁对你的裁决很不满意,决定到图2中的比赛场地再比一次,依然黑蚂蚁沿着大半圆爬,白蚂蚁沿着小半圆爬,同时从A地出发,那么请问哪只蚂蚁先爬到B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
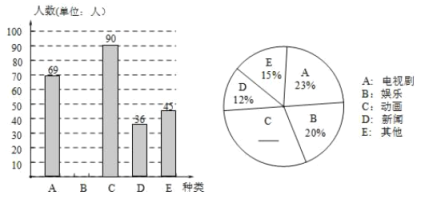
(1)本次调查的学生人数为__________,娱乐节目在扇形统计图中所占圆心角的度数是__________度.
(2)请将条形统计图补充完整:
(3)若该中学有2000名学生,请估计该校喜爱动画节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点 ![]() 对应的数为
对应的数为 ![]() ,点
,点 ![]() 对应的数为
对应的数为 ![]() ,且多项式
,且多项式 ![]() 的二次项系数为
的二次项系数为 ![]() ,常数项为
,常数项为 ![]() .
.
(1)直接写出:![]() ,
,![]() .
.
(2)数轴上点 ![]() ,
,![]() 之间有一动点
之间有一动点 ![]() ,若点
,若点 ![]() 对应的数为
对应的数为 ![]() ,试化简
,试化简 ![]() .
.
(3)若点 ![]() 从点
从点 ![]() 出发,以每秒
出发,以每秒 ![]() 个单位长度的速度沿数轴向右移动;同时点
个单位长度的速度沿数轴向右移动;同时点 ![]() 从点
从点 ![]() 出发,沿数轴以每秒
出发,沿数轴以每秒 ![]() 个单位长度的速度向左移动,到达
个单位长度的速度向左移动,到达 ![]() 点后立即返回并向右继续移动,经过t秒后,
点后立即返回并向右继续移动,经过t秒后,![]() ,
,![]() 两点相距
两点相距 ![]() 个单位长度,求t的值.
个单位长度,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (用如图所示的曲尺形框框(有三个方向),可以套住下表中的三个数,设被框住的三个数中(第一个框框住的最小的数为a、第二个框框住的最小的数为b、第三个框框住的最小的数为c).
(1)第一个框框住的三个数中最小的数为a,三个数的和是: ;第二个框框住的三个数中最小的数为b,三个数的和是: ;第三个框框住的三个数中最小的数为c,三个数的和是: ;
(2)这三个框框住的数的和能是48吗?,能,求出最小的数a、b、c的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
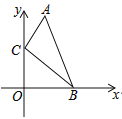
A. (0,0); B. (0,1); C. (0,2); D. (0,3).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com