
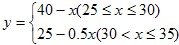
解:(1)∵25≦28≦30,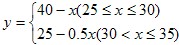 ,
,
∴把28代入y=40﹣x得,
∴y=12(万件),
答:当销售单价定为28元时,该产品的年销售量为12万件;
(2)①当 25≦x≦30时,
W=(40﹣x)(x﹣20)﹣2 5﹣100=﹣x2+60x﹣925=﹣(x﹣30)2﹣25,
5﹣100=﹣x2+60x﹣925=﹣(x﹣30)2﹣25,
故当x=30时,W最大为﹣25,及公司最少亏损25万;
②当30<x≤35时,
W=(25﹣0.5x)(x﹣20)﹣25﹣100=﹣ x2+35x﹣625=﹣
x2+35x﹣625=﹣ (x﹣35)2﹣12.5,
(x﹣35)2﹣12.5,
故当x=35时,W最大为﹣12.5,及公司最少亏损12.5万;
对比①,②得,投资的第一年,公司亏损,最少亏损是12.5万;
答:投资的第一年,公司亏损,最少亏损是12.5万;
(3)①当 25≤x≤30时,
W=(40﹣x)(x﹣20﹣1)﹣12.5﹣10=﹣x2+59x﹣782.5,
令W=67.5,则﹣x2+59x﹣782.5=67.5
化简得:x2﹣59x+850=0 ,
解得: x1=25;x2=34,
此时,当两年的总盈利不低于67.5万元,25≦x≦30;
②当30<x≤35时,
W=(25﹣0.5x)(x ﹣20﹣1)﹣12.5﹣10=﹣
﹣20﹣1)﹣12.5﹣10=﹣ x2+35.5x﹣547.5,
x2+35.5x﹣547.5,
令W=67.5,则﹣ x2+35.5x﹣547.5=67.5,
x2+35.5x﹣547.5=67.5,
化简得:x2﹣71x+1230=0
解得:x1=30;x2=41,
此时,当两年的总盈利不低于67.5万元,30<x≦35,
答:到第二年年底,两年的总盈利不低于67.5万元,此时销售单价的范围是25≦x≦30或
30<x≦35.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
在长株潭建设两型社会的过程中,为推进节能减排,发展低碳经济,我市某公司以25万元购得某项节能产品的生产技术后,再投入100万元购买生产设备,进行该产品的生产加工。已知生产这种产品的成本价为每件20元。经过市场调研发现,该产品的销售单价定在25元到30元之间较为合理,并且该产品的年销售量y(万件)与销售单价x(元)之间的函数关系式为:![]()
(年获利=年销售收入-生产成本-投资成本)
(1) 当销售单价定为28元时,该产品的年销售量为多少万件?
(2) 求该公司第一年的年获利W(万元)与销售单价x(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(3) 第二年,该公司决定给希望工程捐款Z万元,该项捐款由两部分组成:一部分为10万元的固定捐款;另一部分则为每销售一件产品,就抽出一元钱作为捐款。若除去第一年的最大获利(或最小亏损)以及第二年的捐款后,到第二年年底,两年的总盈利不低于67.5万元,请你确定此时销售单价的范围;
查看答案和解析>>
科目:初中数学 来源:2013年湖北省黄石市中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2013年湖北省黄石市阳新一中卓越联盟中考数学模拟试卷(解析版) 题型:解答题
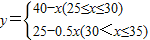
查看答案和解析>>
科目:初中数学 来源:2013年湖北省黄冈市中考数学模拟试卷(十二)(解析版) 题型:解答题
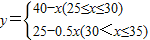
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com