
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
| A. | 4000元,8000元 | B. | 8000元,4000元 | C. | 14000元,8000元 | D. | 10000元,12000元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一位自行车爱好者利用周末进行了一次骑车旅行,如图是这次旅行过程中自行车到出发地的距离y(千米)与骑行时间t(分钟)之间的函数图象,观察图象,下列判断中正确的是( )
一位自行车爱好者利用周末进行了一次骑车旅行,如图是这次旅行过程中自行车到出发地的距离y(千米)与骑行时间t(分钟)之间的函数图象,观察图象,下列判断中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
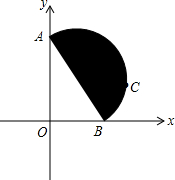 如图,以AB为直径的半圆型铁片按如图所示的位置平放斜靠在坐标轴上,点C是半圆片弧AB上靠近B点的一个定点,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴正方向滑动.请判断:在滑动过程中,点C与点O距离的变化情况是( )
如图,以AB为直径的半圆型铁片按如图所示的位置平放斜靠在坐标轴上,点C是半圆片弧AB上靠近B点的一个定点,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴正方向滑动.请判断:在滑动过程中,点C与点O距离的变化情况是( )| A. | 一直增大 | B. | 保持不变 | C. | 先减小后增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
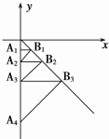 如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,再过点A2作y轴的垂线,交直线y=-x于点B2…则点B4的坐标为($\frac{8}{3}$,-$\frac{8}{3}$).
如图,在平面直角坐标系中,过点A1(0,-$\frac{1}{3}$)作y轴的垂线,交直线y=-x于点B1,再过点B1作直线y=-x的垂线,交y轴于点A2,再过点A2作y轴的垂线,交直线y=-x于点B2…则点B4的坐标为($\frac{8}{3}$,-$\frac{8}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com