
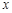 轴交于点C,与双曲线
轴交于点C,与双曲线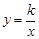 交于A(3,
交于A(3,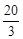 )、B(-5,
)、B(-5,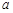 )两点.AD⊥
)两点.AD⊥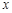 轴于点D,BE∥
轴于点D,BE∥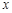 轴且与
轴且与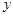 轴交于点E.
轴交于点E. >0时,x的取值范围是 ;
>0时,x的取值范围是 ;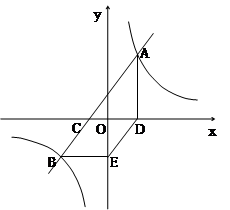
 过A(3,
过A(3, ),∴
),∴ .………………………1分
.………………………1分 )代入
)代入 ,
, . ∴点B的坐标是(-5,-4). --------------------2分
. ∴点B的坐标是(-5,-4). --------------------2分 )、B(-5,-4)代入
)、B(-5,-4)代入 ,得,
,得, , 解得:
, 解得: .
. .………………………………… 3分
.………………………………… 3分 轴, ∴点E的坐标是(0,-4).
轴, ∴点E的坐标是(0,-4). =5,∴ED=CD.
=5,∴ED=CD.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
(本题满分8分)
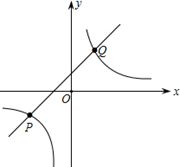
如图,已知一次函数与反比例函数的图象交于点P(-2,-1)和点Q(1,m)
(1)求这两个函数的关系式;
(2)根据图象,直接写出当一次函数的值大于反比例函数的值时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
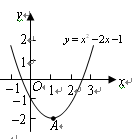
(本题满分10分)如图,已知二次函数![]() 的图象的顶点为
的图象的顶点为![]() .二次函数
.二次函数![]() 的图象与
的图象与![]() 轴交于原点
轴交于原点![]() 及另一点
及另一点![]() ,它的顶点
,它的顶点![]() 在函数
在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1)求点![]() 与点
与点![]() 的坐标;
的坐标;
(2)当四边形![]() 为菱形时,求函数
为菱形时,求函数![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源:2011届广东省中考数学模拟试卷(二) 题型:解答题
(本题满分7分)如图,已知一次函数y=kx +b的图象与反比例函数
+b的图象与反比例函数
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△ABC的面积.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西钦州卷)数学 题型:解答题
(本题满分8分)如图,已知AB是⊙O的 弦,OB=2,∠B=30°,
弦,OB=2,∠B=30°,
C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交
于⊙O于点D,连接AD.
(1)弦长AB等于 ▲ (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、
C、O为顶点的三角形相似?请写出解答过程.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏扬中市九年级下学期期中考试数学试卷(解析版) 题型:解答题
活动探究(本小题满分7分)
如图,已知二次函数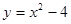 ,将
,将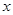 轴下方的图象沿
轴下方的图象沿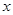 轴翻折,得到一个新图象(图中的实线).
轴翻折,得到一个新图象(图中的实线).
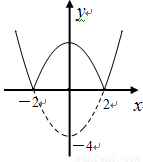
根据新图像回答问题:
(1)当x= ▲ 时,函数y有最小值.
(2)当y随x的增大而增大时,自变量x的范围是 ▲ .
(3)当a<4时,探究一次函数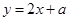 的图像与新图象公共点的个数情况.
的图像与新图象公共点的个数情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com