
 如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m,如果梯子的顶端下滑1m,那么梯子的底端滑动($\sqrt{51}$-6)m.
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m,如果梯子的顶端下滑1m,那么梯子的底端滑动($\sqrt{51}$-6)m. 分析 已知AB,AO,在直角△ABO中即可计算BO,梯子的顶端下滑1米,即CO=7米,CD=AB=10米,在直角△COD中,根据勾股定理即可计算OD,底端滑动的距离为OD-OB,计算即可.
解答 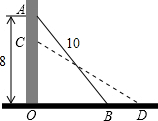 解:在△AOB中,∠AOB=90°,AB=10米,AO=8米,由勾股定理得OB=6米,
解:在△AOB中,∠AOB=90°,AB=10米,AO=8米,由勾股定理得OB=6米,
△COD中,∠C=90°,AB=10米,CO=7米,由勾股定理得OD=$\sqrt{1{0}^{2}-{7}^{2}}$=$\sqrt{51}$米,
∴BD=OD-OB=$\sqrt{51}$-6(米),
∴梯子底端滑动($\sqrt{51}$-6)米.
故答案为($\sqrt{51}$-6).
点评 本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是( )
如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是( )| A. | 2:1 | B. | 1:2 | C. | 4:1 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线的顶点为(2,-1),且过(1,0)点.
已知抛物线的顶点为(2,-1),且过(1,0)点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V(cm3) | 324 | 512 | 588 | 576 | 500 | 384 | 252 | 128 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com