
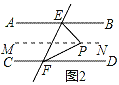
【题目】已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB_____.
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD_____.
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
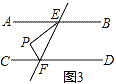
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
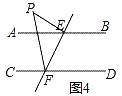
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:_____.

【答案】两直线平行,内错角相等如果两条直线都和第三条直线平行,那么这两条直线也互相平行∠EPM∠MPF∠EPF+∠PFD=∠PEB
【解析】
(1)根据对顶角相等可得∠BEF的度数,根据同旁内角互补,两直线平行,即可得出结论;
(2)①过点P作MN∥AB,根据平行线的性质得∠EPM=∠PEB,且有MN∥CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB+∠PFD.
②③的解题方法与①一样,分别过点P作MN∥AB,然后利用平行线的性质得到三个角之间的关系.
(1)∵∠1=120°,
∴∠BEF=120°,
又∵∠2=60°,
∴∠2+∠BEF=180°,
∴AB∥CD;

(2)①如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等).
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD(平行于同一条直线的两条直线互相平行).
∴∠MPF=∠PFD,
∴∠EPM+∠FPM=∠PEB+∠PFD(等式的性质),
即∠EPF=∠PEB+∠PFD,
故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;∠EPM,∠MPF;
②∠EPF+∠PEB+∠PFD=360°;
证明:如图3,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠BEP+∠EPM=180°,∠DFP+∠FPM=180°,
∴∠BEP+∠EPM+∠FPM+∠PFD=360°,
即∠EPF+∠PEB+∠PFD=360°;

③∠EPF+∠PFD=∠PEB.
理由:如图4,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠PEB=∠MPE,∠PFD=∠MPF,
∵∠EPF+∠FPM=∠MPE,
∴∠EPF+∠PFD=∠PEB.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某汽车专买店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的件价各为多少万元;
每辆A型车和B型车的售价分别是x万元,y万元.
根据题意,列方程组
解这个方程组,得x= ,y=
答: .
(2)有一家公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过130万元,求这次购进B型车最多几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
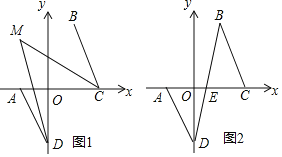
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是(填编号) 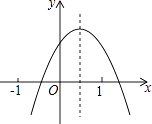
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示表示王勇同学骑自行车离家的距离与时间之间的关系,王勇9点离开家,15点回家,请结合图象,回答下列问题:
![]() 到达离家最远的地方是什么时间?离家多远?
到达离家最远的地方是什么时间?离家多远?
![]() 他一共休息了几次?休息时间最长的一次是多长时间?
他一共休息了几次?休息时间最长的一次是多长时间?
![]() 在哪些时间段内,他骑车的速度最快?最快速度是多少?
在哪些时间段内,他骑车的速度最快?最快速度是多少?
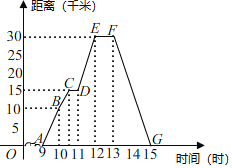
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
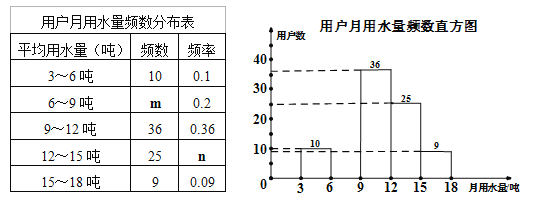
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= ;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 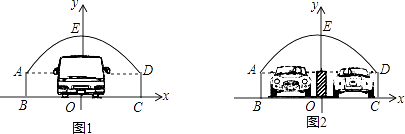
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com