
【题目】解下列方程: (1)x2-49=0 (2)3x2-7x=0 (3)(2x-1)2=9
(4)x2+3x-4=0 (5)(x+4)2=5(x+4) (6)x2+4x=2
【答案】(1)±7;(2)0,![]() ;(3)2,-1;(4)-4,1;(5)-4,1 ;(6)-2±
;(3)2,-1;(4)-4,1;(5)-4,1 ;(6)-2±![]() .
.
【解析】
(1)运用平方差公式分解因式,即可得出两个一元一次方程,求出方程的解即可;;
(2)运用提公因式法分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)直接开平方,即可得出两个一元一次方程,求出方程的解即可;
(4)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(5)先把方程整理成一般形式,再因式分解,即可得出两个一元一次方程,求出方程的解即可;
(6)移项后运用公式法即可得出方程的解;
(1)x2-49=0
(x+7)(x-7)=0
∴x1=7,x2=-7;
(2)3x2-7x=0
x(3x-7)=0
∴x1=0,x2=![]() ;
;
(3)(2x-1)2=9
2x-1=![]()
2x-1=3或2x-1=-3
∴x1=2,x2=-1;
(4)x2+3x-4=0
(x+4)(x-1)=0
∴ x1=-4,x2=1;
(5)(x+4)2=5(x+4)
x2+8x+16=5x+20
x2+3x-4=0
(x+4)(x-1)=0
∴x1=-4,x2=1;
(6)x2+4x=2
x2+4x-2=0
b2-4ac=16+8=24,
∴x1=-2+![]() ,x2=-2-
,x2=-2-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
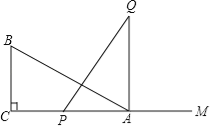
【题目】如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校2400名学生对某次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图①)、扇形统计图(图②)和折线统计图(图③).

(1)本次共随机抽查了________名学生,根据信息补全图①中条形统计图,图②中八年级所对应扇形的圆心角的度数为________;
(2)如果把“特别关注”“一般关注”“偶尔关注”都看成关注,那么全校关注足球赛的学生大约有多少名?
(3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议;
②如果要了解中小学生对校园足球的关注情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C所对的边分别是![]() ,下列条件中,不能判定△ABC是等腰三角形的是( )
,下列条件中,不能判定△ABC是等腰三角形的是( )
A.a3,b3,c4B.a︰b︰c2︰3︰4
C.∠B50°,∠C80°D.∠A︰∠B︰∠C1︰1︰2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
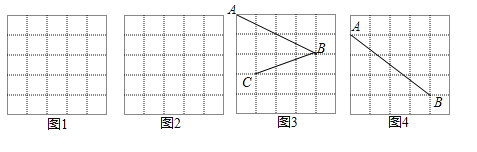
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点的画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2,![]()
(3)如图3,点A,B,C是格点,则∠ABC= ;
(4)在图4中画出△ABC(点C是格点),使△ABC为等腰三角形(画一个).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com