
【题目】将矩形纸片![]() 按如图的方式折叠,得到菱形
按如图的方式折叠,得到菱形![]() ,若
,若![]() ,则
,则![]() 的长为( )
的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求解.
解:∵菱形AECF,AB=3,
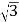
∴假设BE=x,
∴AE=3-x,
∴CE=3-x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=3-x,
解得:x=1,
∴CE=2,利用勾股定理得出:
BC2+BE2=EC2,
BC=![]() =
=![]() =
=![]() ,
,
故选:D.
此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.


科目:初中数学 来源: 题型:
【题目】如图所示,在数轴上点![]() 表示的数分别为-2,0,6,点
表示的数分别为-2,0,6,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .
.
(1)填空:![]() ;
;
(2)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度,5个单位长度的速度向右运动.
分别以每秒2个单位长度,5个单位长度的速度向右运动.
①设运动时间为![]() ,请用含有
,请用含有![]() 的算式分别表示出
的算式分别表示出![]() ;
;
②在①的条件下,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而变化?若变化,请说明理由;若不变,请求其值.
的变化而变化?若变化,请说明理由;若不变,请求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某学校为了改善办学条件,计划采购A,B两种型号的空调,已知采购3台A型空调和2台B型空调共需3.9万元;采购4台A型空调比采购5台B空调的费用多0.6万元.
(1)求A型空调和B型空调每台各需多少万元;
(2)若学校计划采购A,B两种型号空调共30台,且采购总费用不少于20万元不足21万元,请求出共有那些采购方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀1min叫的次数除以7,然后再加上3,就近似地得到该地当时的温度(℃).
(1)用代数式表示该地当时的温度;
(2)当蟋蟀1min叫的次数分别是84,105和126时,该地当时的温度约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).
(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为![]() 盒时,在甲店购买需付款 元;在乙店购买需付款 元.
盒时,在甲店购买需付款 元;在乙店购买需付款 元.
(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.
(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,张明同学想测量某铜像的高度,已知铜像(图中![]() )高度比底座(图中
)高度比底座(图中![]() )高度多1米,张明随后用高度为1米的测角仪(图中
)高度多1米,张明随后用高度为1米的测角仪(图中![]() )测得铜像顶端点
)测得铜像顶端点![]() 的仰角β=51°24′,底座顶端点
的仰角β=51°24′,底座顶端点![]() 的仰角
的仰角![]() =26°36′.请你帮助张明算出铜像AB的高度(把铜像和底座近似看在一条直线上它的抽象几何图形如左图).(参考数据:sin26°36′≈0.45, cos26°36′≈0.89,tan26°36′≈0.5,sin51°24′≈0.78,cos51°24′≈0.6,tan51°24′≈1.25)
=26°36′.请你帮助张明算出铜像AB的高度(把铜像和底座近似看在一条直线上它的抽象几何图形如左图).(参考数据:sin26°36′≈0.45, cos26°36′≈0.89,tan26°36′≈0.5,sin51°24′≈0.78,cos51°24′≈0.6,tan51°24′≈1.25)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com