
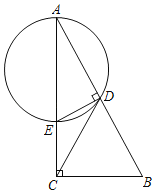
【题目】如图,已知Rt△ABC中,∠ACB=90°,E为AB上一点,以AE为直径作⊙O与BC相切于点D,连接ED并延长交AC的延长线于点F.
(1)求证:AE=AF;
(2)若AE=5,AC=4,求BE的长.
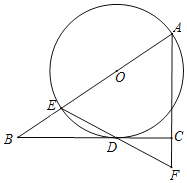
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
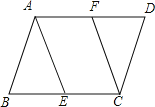
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
查看答案和解析>>
科目:初中数学 来源: 题型:
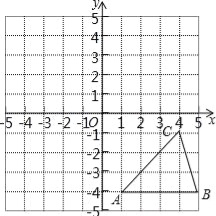
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)作出△ABC关于y轴对称的![]() ,并写出
,并写出![]() 的坐标;
的坐标;
(2)作出△ABC绕点O逆时针旋转90°后得到的![]() ,并求出
,并求出![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B. 从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C. 某彩票中奖率为![]() ,说明买100张彩票,有36张中奖。
,说明买100张彩票,有36张中奖。
D. 打开电视,中央一套正在播放新闻联播。
查看答案和解析>>
科目:初中数学 来源: 题型:
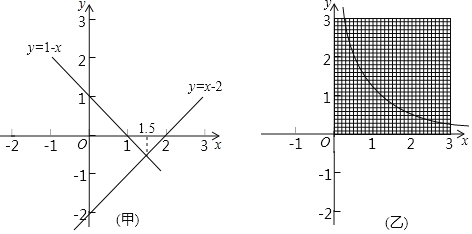
【题目】我们知道、可以借助于函数图象求方程的近似解,如图(甲),把方程x﹣2=1﹣x的解看成函数y=x﹣2的图象与函数y=1﹣x的图象的交点的横坐标,求得方程x﹣2=1﹣x的解为x=1.5,如图(乙),已画出了反比例函数y![]() 在第一象限内的图象,借助于此图象求出方程x2﹣x
在第一象限内的图象,借助于此图象求出方程x2﹣x![]() 0的正数解.(要求画出相应函数的图象,结果精确到0.1)
0的正数解.(要求画出相应函数的图象,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
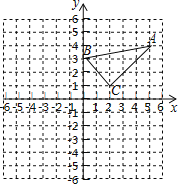
(1)画出△ABC关于原点成中心对称的△A1B1C1,并写出点C1的坐标;
(2)画出将A1B1C1绕点C1按顺时针旋转90°所得的△A2B2C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD为斜边AB的中线.过点D作AB的垂线交AC于点E,再过A、D、E三点作⊙O.
(1)确定⊙O的圆心O的位置,并证明CD为⊙O的切线;
(2)若BC=3,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com