
分析 (1)设A型台灯购进x盏,则B型台灯购进3x盏,根据A型节能台灯的进货单价比B型的进货单价少20元,列方程求解;
(2)设购进B型台灯m盏,根据商场购进100盏台灯且规定B型台灯的进货数量不超过A型台灯数量的2倍,列不等式求解,进一步得到商场在销售完这批台灯时获利最多时的利润.
解答 解:(1)设A型台灯购进x盏,则B型台灯购进3x盏,依题意有
$\frac{500}{x}$+20=$\frac{3000}{3x}$,
解得:x=25.
经检验,x=25是原方程的解,
3x=3×25=75.
故A型台灯购进25盏,则B型台灯购进75盏.
(2)设购进B型台灯m盏,依题意有
m≤2(100-m),
解得m≤66$\frac{2}{3}$,
35-20=15(元),
60-(20+20)=20(元),
∵m为整数,15<20,
∴m=66,即A型台灯购进34盏,B型台灯购进66盏时获利最多,
34×15+20×66
=510+1320
=1830(元).
此时利润为1830元.
点评 本题考查了分式方程的应用和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | 5和6 | B. | 6和7 | C. | 7和8 | D. | 8和9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
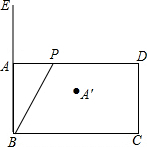 如图,矩形ABCD中,AB=2,BC=2$\sqrt{3}$,动点P从A点出发,沿AD运动到D点,连接BP,点A关于直线BP的对称点为A′,
如图,矩形ABCD中,AB=2,BC=2$\sqrt{3}$,动点P从A点出发,沿AD运动到D点,连接BP,点A关于直线BP的对称点为A′,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com