
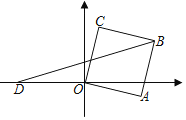
【题目】如图,正方形ABCO的边长为![]() ,OA与x轴正半轴的夹角为15°,点B在第一象限,点D在x轴的负半轴上,且满足∠BDO=15°,直线y=kx+b经过B、D两点,则b﹣k=_____.
,OA与x轴正半轴的夹角为15°,点B在第一象限,点D在x轴的负半轴上,且满足∠BDO=15°,直线y=kx+b经过B、D两点,则b﹣k=_____.
【答案】2﹣![]() .
.
【解析】
连接OB,过点B作BE⊥x轴于点E,根据正方形的性质可得出∠AOB的度数及OB的长,结合三角形外角的性质可得出∠BDO=∠DBO,利用等角对等边可得出OD=OB,进而可得出点D的坐标,在Rt△BOE中,通过解直角三角形可得出点B的坐标,由点B,D的坐标,利用待定系数法可求出k,b的值,再将其代入(b﹣k)中即可求出结论.
解:连接OB,过点B作BE⊥x轴于点E,如图所示.
∵正方形ABCO的边长为![]() ,
,
∴∠AOB=45°,OB=![]() OA=2.
OA=2.
∵OA与x轴正半轴的夹角为15°,
∴∠BOE=45°﹣15°=30°.
又∵∠BDO=15°,
∴∠DBO=∠BOE﹣∠BDO=15°,
∴∠BDO=∠DBO,
∴OD=OB=2,
∴点D的坐标为(﹣2,0).
在Rt△BOE中,OB=2,∠BOE=30°,
∴BE=![]() OB=1,OE=
OB=1,OE=![]() =
=![]() ,
,
∴点B的坐标为(![]() ,1).
,1).
将B(![]() ,1),D(﹣2,0)代入y=kx+b,
,1),D(﹣2,0)代入y=kx+b,
得: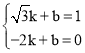 ,
,
解得: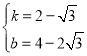 ,
,
∴b﹣k=4﹣2![]() ﹣(2﹣
﹣(2﹣![]() )=2﹣
)=2﹣![]() .
.
故答案为:2﹣![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△A'B'C',设点B的对应点B'的横坐标为2,则点B的横坐标为( )
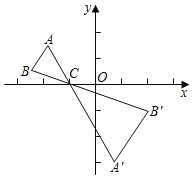
A.﹣1B.![]() C.﹣2D.
C.﹣2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作)BD是矩形ABCD的对角线,AB=4,BC=3.将△BAD绕着点B顺时针旋转α度(0°<α<360°)得到△BEF,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则DE=______.
(探究)当点E落在线段DF上时,CD与BE交于点G.其它条件不变,如图②.
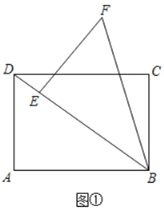
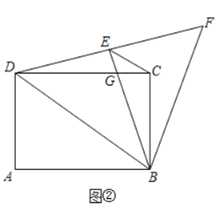
(1)求证:△ADB≌△EDB;
(2)CG的长为______.
(拓展)连结CF,在△BAD的旋转过程中,设△CEF的面积为S,直接写出S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
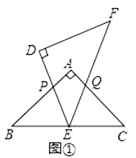
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
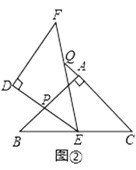
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;
(3)在(2)的条件下,BP=2,CQ=9,则BC的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.
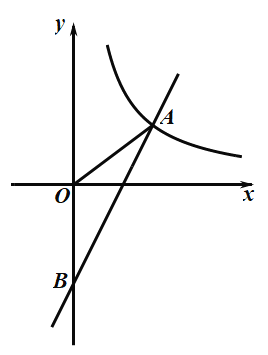
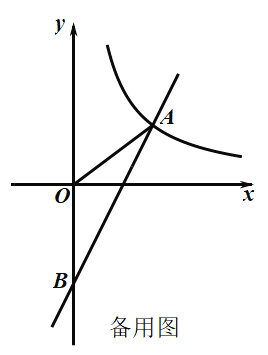
(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP',连接CP',则线段CP'的最小值为( )
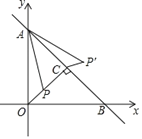
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
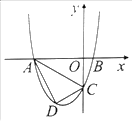
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
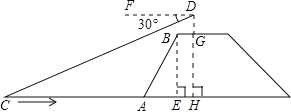
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长.(参考数据:![]() ≈1.7,结果保留一位小数)
≈1.7,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=(ax-1)(x-a),其中a是常数,且a≠0.
(1)当a=2时,试判断点(-![]() ,-5)是否在该函数图象上.
,-5)是否在该函数图象上.
(2)若函数的图象经过点(1,-4),求该函数的表达式.
(3)当![]() -1≤x≤
-1≤x≤![]() +1时,y随x的增大而减小,求a的取值范围.
+1时,y随x的增大而减小,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com