
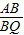 =
=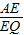 =2
=2
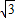

 (4
(4 +2
+2 )×6=18
)×6=18 .
.

科目:初中数学 来源:2009年江苏省盐城市大丰市中考数学一模试卷(解析版) 题型:解答题
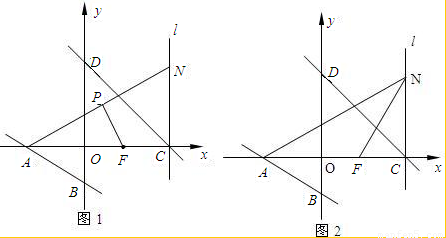
查看答案和解析>>
科目:初中数学 来源:2009年江苏省泰州市泰兴市四校联考试卷(解析版) 题型:解答题
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= 计算结果保留根号)
计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2009年江苏省泰州市泰兴市四校联考试卷(解析版) 题型:选择题
 ,侧面展开图是半圆,则圆锥的侧面积为( )
,侧面展开图是半圆,则圆锥的侧面积为( )查看答案和解析>>
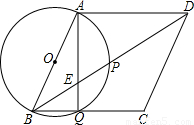
科目:初中数学 来源:2009年湖北省荆州市沙市区中考数学二模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com