
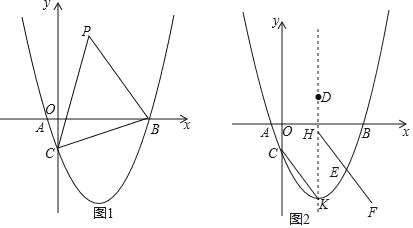
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У������� y=![]() x2��
x2��![]() x��
x��![]() ��x�ύ��A��B�����㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��x�ύ��A��B�����㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��1���ж���ABC��״����˵�����ɣ�
��2���������ߵ�����������һ�㣬������x��ĶԳƵ��Ϊ��P����M��ֱ��BC�ϵ�һ���㣬����PBC��������ʱ����PM+![]() MC����Сֵ��
MC����Сֵ��
��3����ͼ2����KΪ�����ߵĶ��㣬��D�������߶Գ�������������Ϊ![]() ���Գ����Ҳ������������һ����E������E��EH��CK�����Գ����ڵ�H���ӳ�HE����F��ʹ��EF=
���Գ����Ҳ������������һ����E������E��EH��CK�����Գ����ڵ�H���ӳ�HE����F��ʹ��EF=![]() ����ƽ������һ��Q��ʹ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ�� �ǶԳ��ᣬ�����Ƿ���������ĵ�Q����������ֱ��д����E�ĺ����꣬�������ڣ���˵�����ɣ�
����ƽ������һ��Q��ʹ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ�� �ǶԳ��ᣬ�����Ƿ���������ĵ�Q����������ֱ��д����E�ĺ����꣬�������ڣ���˵�����ɣ�
���𰸡���1�����ۣ���ABC��ֱ����������2��![]() ��3�����ڣ����������ĵ�E�ĺ�����Ϊ
��3�����ڣ����������ĵ�E�ĺ�����Ϊ![]() ��
��![]() ��
��![]() ��
��![]()
�������������������1���ɡ�AOC�ס�COB���Ƴ���ACO=��OBC���ɡ�OBC+��OCB=90�㣬�Ƴ���ACO+��BCO=90�㣬�Ƴ���ACB=90�㣬�ó����ۣ�
��2����ͼ1�У������������������һ��N��m�� ![]() x2��
x2��![]() x��
x��![]() ������N����x��ĶԳƵ�P��m��-
������N����x��ĶԳƵ�P��m��-![]() x2+
x2+![]() x+
x+![]() ��������B��C�ֱ���y�ᡢx���ƽ���߽��ڵ�G������PG���ɵ�S��PBC=S��PCG+S��PBG��S��BCG���ɴ˿ɵá�PBC������ʱ�ĵ�P�����꣬��ͼ2����ME��CG�ڵ�M���ɡ�CEM�ס�BOC�����ݶ�Ӧ�߳ɱ������ó�PM+
��������B��C�ֱ���y�ᡢx���ƽ���߽��ڵ�G������PG���ɵ�S��PBC=S��PCG+S��PBG��S��BCG���ɴ˿ɵá�PBC������ʱ�ĵ�P�����꣬��ͼ2����ME��CG�ڵ�M���ɡ�CEM�ס�BOC�����ݶ�Ӧ�߳ɱ������ó�PM+![]() CM=PM+ME�����ݴ��߶���̿�֪����PE��CGʱ��PM+ME��̣��ɴ˼��ɽ����
CM=PM+ME�����ݴ��߶���̿�֪����PE��CGʱ��PM+ME��̣��ɴ˼��ɽ����
��3��������������ۣ�����ͼ3����DH=HF��HQƽ�֡�DHFʱ������F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ���ǶԳ��ᣬ����ͼ4����DH=HF��HQƽ�֡�DHFʱ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ���ǶԳ��ᣬ����ͼ5����DH=DF��DQƽ�֡�HDFʱ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ���ǶԳ��ᣬ�ֱ���⼴��.
�����������1�����ۣ���ABC��ֱ�������Σ��������£�
���������� y=![]() x2��
x2��![]() x��
x��![]() ����y=0��
����y=0�� ![]() x2��
x2��![]() x��
x��![]() =0�����x=��
=0�����x=��![]() ��3
��3![]() ����x=0��y=��
����x=0��y=��![]() ��
��
��A����![]() ��0����C��0����
��0����C��0����![]() ����B��3
����B��3![]() ��0����
��0����
��OA=![]() ��OC=
��OC=![]() ��OB=3
��OB=3![]() ��
��
��![]() =
=![]() =
=![]() ���ߡ�AOC=��BOC��
���ߡ�AOC=��BOC��
���AOC�ס�COB��
���ACO=��OBC��
�ߡ�OBC+��OCB=90�㣬
���ACO+��BCO=90�㣬
���ACB=90�㣮
��Ҳ�������AC��BC��AB���ù��ɶ������涨��֤������
��2����ͼ1�У������������������һ��N��m��![]() m2��
m2��![]() m��
m��![]() ������N����x��ĶԳƵ�P��m����
������N����x��ĶԳƵ�P��m����![]() m2+
m2+![]() m+
m+![]() ��������B��C�ֱ���y�ᣬx���ƽ���߽��ڵ�G������PG��
��������B��C�ֱ���y�ᣬx���ƽ���߽��ڵ�G������PG��
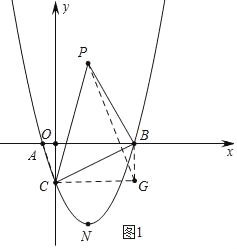
��G��3![]() ����
����![]() ����
����
��S��PBC=S��PCG+S��PBG��S��BCG=![]() ��
��![]() ������
������![]() m2+
m2+![]() m+2
m+2![]() ��+
��+![]() ��
��![]() ��3
��3![]() ��m����
��m����![]() ��
��![]() ��
��![]() =��
=��![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
�ߩ�![]() ��0��
��0��
�൱m=![]() ʱ����PBC��������
ʱ����PBC��������
��ʱP��![]() ��
��![]() ����
����
��ͼ2�У���ME��CG��M��
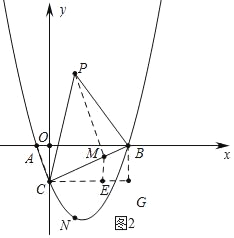
��CG��OB��
���OBC=��ECM���ߡ�BOC=��CEM��
���CEM�ס�BOC��
��OC��OB��BC=1��3��![]() ��
��
��EM��CE��CM=1��3��![]() ��
��
��EM=![]() CM��
CM��
��PM+![]() CM=PM+ME��
CM=PM+ME��
����ݴ��߶���̿�֪����PE��CGʱ��PM+ME��̣�
��PM+![]() MC����СֵΪ
MC����СֵΪ![]() +
+![]() =
=![]() ��
��
��3�����ڣ��������£�
����ͼ3�У���DH=HF��HQƽ�֡�DHFʱ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ�� �ǶԳ��ᣮ
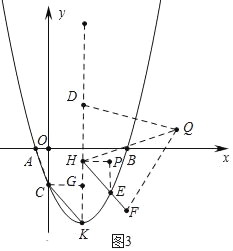
��CG��HK��G��PH��x�ᣬEP��PH��P��
��FH��CK��K��![]()
![]() ����
����![]()
![]() ����
����
��֪CG��GK��CK=3��4��5��
�ɡ�EPH�ס�KGC����PH��PE��EH=3��4��5����E����n��![]() n2��
n2��![]() n��
n��![]() ������HE=
������HE=![]() ��n��
��n��![]()
![]() ����PE=
����PE=![]() ��n��
��n��![]()
![]() ����
����
��DH=HF��
��![]() +[��
+[��![]() n2+
n2+![]() n+
n+![]() ��
��![]() ��n��
��n��![]()
![]() ��]=
��]=![]() ��n��
��n��![]()
![]() ��+
��+![]()
![]() ��
��
���n=![]() ��
��![]() ����������
����������
����ͼ4�У���DH=HF��HQƽ�֡�DHFʱ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ�� �ǶԳ��ᣮ

ͬ���ɵ�[![]() n2��
n2��![]() n��
n��![]() +
+![]() ��n��
��n��![]()
![]() ��]��
��]��![]() =
=![]() ��n��
��n��![]()
![]() ��+
��+![]()
![]() ��
��
���n=![]() +
+![]() ��
��![]() ��
��![]() ����������
����������
����ͼ5�У���DH=DF��DQƽ�֡�HDFʱ���Ե�F��H��D��QΪ������ı�������Գ�ͼ�Σ��ҹ���Q�ĶԽ������ڵ�ֱ�� �ǶԳ��ᣮ
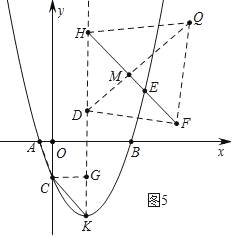
��DQ��HF��M���ɡ�DHM�ס�CKG����֪HM��DH=4��5��
![]() [
[![]() ��n��
��n��![]()
![]() ��+
��+![]()
![]() ]��[
]��[![]() n2��
n2��![]() n��
n��![]() +
+![]() ��n��
��n��![]()
![]() ����
����![]() ]=4��5��
]=4��5��
���n=![]() +
+![]() ��=
��=![]() ��
��![]() ����������
����������
����ͼ6�У���FQƽ�֡�DFHʱ��������������ʱ![]() =
=![]() ��
��
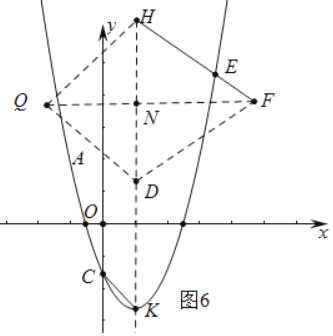
��5��![]() [
[![]() n2��
n2��![]() n��
n��![]() ��
��![]() +
+![]() ��n��
��n��![]()
![]() ��]=4[
��]=4[![]() ��n��
��n��![]()
![]() ��+
��+![]()
![]() ]��
]��
��ã�n=![]() ��
��![]() ��������
��������
�����������������ĵ�E�ĺ�����Ϊ![]() ��
��![]() +
+![]() ��
��![]() +
+![]() ��
��![]() ��
��


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
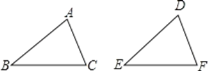
����Ŀ����ͼ����������������������AB=DE��BC=EF��AC=DF�� ��AB=DE����B=��E��BC=EF���ۡ�B=��E��BC=EF����C=��F�� ��AB=DE��AC=DF����B=��E����ʹ��ABC�ա�DEF��_____�飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��9a+c��3b����3��8a+7b+2c��0����4������A����3��y1������B����![]() ��y2������C��
��y2������C��![]() ��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������
��y3���ڸú���ͼ���ϣ���y1��y3��y2����5��������a��x+1����x��5��=��3������Ϊx1��x2����x1��x2����x1����1��5��x2��������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ĵ����ϣ�10����ȫ��ͬ���ⳤΪ2cm��С������ѳ�һ�������壮
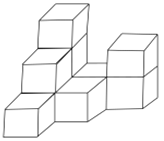
��1�����������濴�ʹ����濴����״ͼ��
��2����������������ı���(��������)���ϻ�ɫ���ᣬ������������������Ƕ���cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ��.
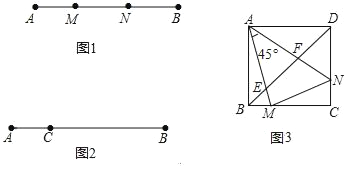
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��AM=3��MN=4��BN�ij���
��2����֪��C���߶�AB�ϵ�һ���㣬��λ����ͼ2��ʾ������BC�ϻ�һ��D��ʹC��D���߶�AB�Ĺ��ɷָ�㣨Ҫ��߹���ͼ��������ͼ�ۼ�������һ�����μ��ɣ���
��3����ͼ3��������ABCD�У�M��N�ֱ���BC��DC�ϣ���BM��DN����MAN=45�㣬AM��AN�ֱ�BD��E��F.
��֤����E��F���߶�BD�Ĺ��ɷָ�㣻
�ڡ�AMN���������AEF�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ���Ƴ���������ͳ��ͼ��
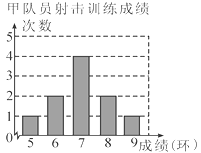
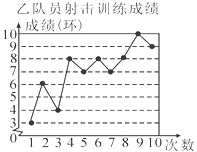
����������Ϣ�����������������£�
ƽ���ɼ�(��) | ��λ��(��) | ����(��) | ���� | |
�� | a | 7 | 7 | 1.2 |
�� | 7 | b | 8 | c |
��1��д��������a��b��c��ֵ��
��2���ֱ����ñ��е��ĸ�ͳ��������Ҫ������������Ա������ɼ�����ѡ������һ������������ΪӦѡ������Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��F�ֱ��DZ�AD��BC�ϵĵ㣬��AE=CF��ֱ��EF�ֱ�BA���ӳ��ߡ�DC���ӳ����ڵ�G��H����BD�ڵ�O��
��1����֤����ABE�ա�CDF��
��2������DG����DG=BG�����ı���BEDF��ʲô�����ı��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и�ʽ��ֵ��
��1����![]() +
+![]() ����
����![]()
��2������3��2��|��![]() |+
|+![]() ��
��![]()
��3��x2��121=0��
��4����x��5��3+8=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() ������
������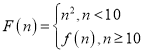 ������
������![]() ��ʾ
��ʾ![]() ����λ���֡�ĩλ���ֵ�ƽ���ͣ����磺
����λ���֡�ĩλ���ֵ�ƽ���ͣ����磺![]() ��
��![]() ���涨
���涨![]() ��
��![]() ��
��![]() Ϊ�������������磬
Ϊ�������������磬![]() ��
��![]() �����˶��壬����
�����˶��壬����![]() __________��
__________��![]() ___________��
___________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com