
【题目】如图,AB为⊙O的直径,C为![]() 上一点,AD∥OC, AD交⊙O于点D,连接AC,CD,设∠BOC=x°,∠ACD=y°,则下列结论成立的是( )
上一点,AD∥OC, AD交⊙O于点D,连接AC,CD,设∠BOC=x°,∠ACD=y°,则下列结论成立的是( )
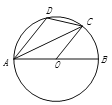
A. x+y=90 B. 2x+y=90 C. 2x+y=180 D. x=y
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )

A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
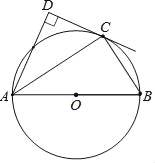
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(1) 采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(2) 求摸出的两个球号码之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节是我国传统佳节,圆圆同学带了4个月饼(除馅不同外,其它均相同),其中有两个火腿馅月饼、一个蛋黄馅和一个枣泥馅月饼.
(1)请你根据上述描述,写出一个不可能事件.
(2)圆圆准备从中任意拿出两个送给她的好朋友月月.
①用树状图或列表的方法列出圆圆拿到两个月饼的所有可能结果;
②请你计算圆圆拿到的两个月饼都是火腿馅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.
(1)若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;
(2)若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们越来越注重营养健康,有一种有机水果![]() 在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克
在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克![]() 水果,立即将其冷藏,请根据下列信息解决问题:
水果,立即将其冷藏,请根据下列信息解决问题:
①水果![]() 的市场价每天每千克上涨0.1元;
的市场价每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天;
(1)若将这批![]() 水果存放
水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为 元;
天后这批水果的销售单价为 元;
(2)将这批![]() 水果存放多少天后一次性出售所得利润为9600元?
水果存放多少天后一次性出售所得利润为9600元?
(3)将这批![]() 水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.

(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得![]() = tanD=
= tanD=![]() ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得![]() ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
试题解析:(1)证明:作OF⊥AB于F

∵AO是∠BAC的角平分线,∠ACB=90
∴OC=OF
∴AB是⊙O的切线
(2)连接CE

∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴![]() = tanD=
= tanD=![]()
(3)先在△ACO中,设AE=x,
由勾股定理得
(x+3)="(2x)" +3 ,解得x="2,"
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得![]() ,
,
设BO=y BF=z
![]()
即4z=9+3y,4y=12+3z
解得z=![]() y=
y=![]()
∴AB=![]() +4=
+4=![]()
考点:圆的综合题.
【题型】解答题
【结束】
22
【题目】已知:二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
(1)求此二次函数的表达式;
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com