
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE. 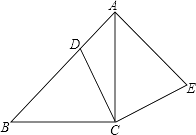
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
【答案】
(1)证明:∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴∠DCE=90°,CD=CE,
∵∠ACB=90°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中
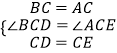 ,
,
∴△BCD≌△ACE,
∴∠B=∠CAE=45°,
∴∠BAE=45°+45°=90°,
∴AB⊥AE;
(2)证明:∵BC2=ADAB,
而BC=AC,
∴AC2=ADAB,
∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,
∴四边形ADCE为矩形,
∵CD=CE,
∴四边形ADCE为正方形.
【解析】(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论;(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形.
【考点精析】关于本题考查的等腰直角三角形和正方形的判定方法,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能得出正确答案.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为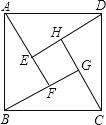
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是反比例函数y= ![]() (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )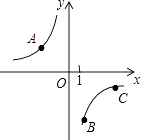
A.4条
B.3条
C.2条
D.1条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读】
如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)【理解】
若点D与点A重合,则这个操作过程为FZ[ , ];
(2)【尝试】
若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)【探究】
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
查看答案和解析>>
科目:初中数学 来源: 题型:
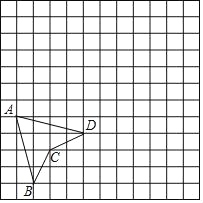
【题目】如图,方格纸中每个小正方形的边长为1,四边形ABCD的顶点都在格点上.
(1)在方格纸上建立平面直角坐标系,使四边形ABCD的顶点A,C的坐标分别为(﹣5,﹣1),(﹣3,﹣3),并写出点D的坐标;
(2)在(1)中所建坐标系中,画出四边形ABCD关于x轴的对称图形A1B1C1D1,并写出点B的对应点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB. 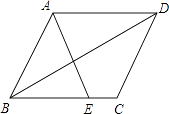
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ![]() x2+bx﹣
x2+bx﹣ ![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com