先阅读短文,再解答短文后面的问题.
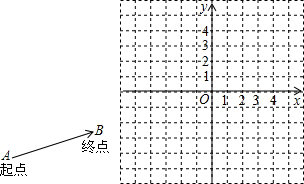
规定了方向的线段称为有向线段.比如,对于线段AB,规定以A为起点,B为终点,便可得到一条从A到B的有向线段.为强调其方向,我们在其终点B处画上箭头(如下图-1).以A为起点,B为终点的有向线段记为
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
|.显然,有向线段
和有向线段
长度相同.方向不同,它们不是同一条有向线段.
对于同一平面内的有向线段,我们可以在该平面建立直角坐标系进行研究(一般情况,直角坐标系的单位长度与有向线段的单位长度相同).比如,以坐标原点O(0,0)为起点,P(3,0)为终点的有向线段
,其方向与x轴正方向相同,长度(或模)是|
|=3.
问题:
(1)在如图所示的平面直角坐标系中画出
有向线段,使得
=3
,
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
(2)若有向线段
的终点B的坐标为(3,
),试求出它的模及它与x轴正半轴的夹角;
(3)若点M、A、P在同一直线上,
||+||=||成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)

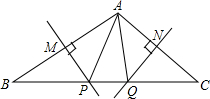 如图所示,若MP和NQ分别垂直平分AB和AC.
如图所示,若MP和NQ分别垂直平分AB和AC.

 口算题天天练系列答案
口算题天天练系列答案